로지스틱 회귀: Difference between revisions

From IT위키
(로지스틱 회귀 분석에 대한 넘겨주기를 제거함)
Tag: Removed redirect
No edit summary
 
(2 intermediate revisions by the same user not shown)
Line 1: Line 1:
[[분류:데이터 과학]]
'''Logistic Regression'''
;Logistic Regression
;분석 대상들이 여러 집단으로 나누어진 경우, 독립 변수의 선형 결합을 이용하여 개별 관측치가 어느 집단에 속하는지 확률을 계산하는 모델


* 로지스틱: 합격/불합격, 성공/실패, 생존/사망, 진실/거짓 등 이분법적인 결과를 도출하기 위한 경우
로지스틱 회귀는 이진 분류 문제를 해결하는 데 많이 사용되는 통계 및 머신러닝 기법이다. 이 알고리즘은 독립 변수들의 선형 조합을 통해 결과 변수(종속 변수)가 특정 클래스에 속할 확률을 예측한다. 주로 0 또는 1로 레이블된 이진 분류에서 활용되지만, 다중 클래스 확장도 가능하다.
* 회귀분석: 과거의 추세를 기반으로 미래 예측
** 로지스틱 회귀분석은 종속변수가 범주형이므로, 분류모델에 더 가까움


== 사용 함수 ==
*'''로지스틱''': 합격/불합격, 성공/실패, 생존/사망, 진실/거짓 등 이분법적인 결과를 도출하기 위한 경우
*'''회귀분석''': 과거의 추세를 기반으로 미래 예측
**로지스틱 회귀분석은 종속변수가 범주형이므로, 분류모델에 더 가까움
 
==사용 함수==
{| class="wikitable"
{| class="wikitable"
|-
|-
! 함수 !! 모양
!함수!!모양
|-
|-
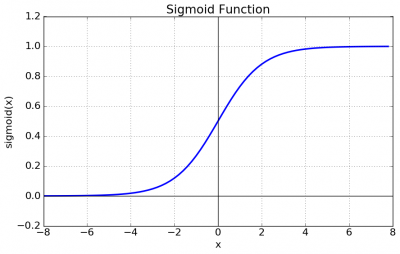
| 시그모이드
|시그모이드
1/(1+e^(-x))  
1/(1+e^(-x))  
||  
||
[[파일:Sigmoid.png|400px]]
[[File:Sigmoid.png|400x400px]]
|-
|-
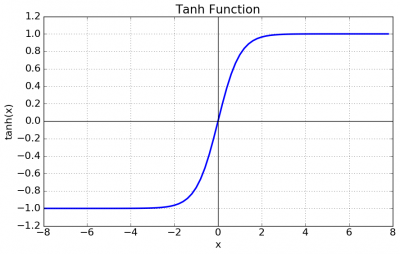
| 하이퍼볼릭 탄젠트
|하이퍼볼릭 탄젠트
tanh(x)  
tanh(x)  
||  
||
[[파일:Tanh.png|400px]]
[[File:Tanh.png|400x400px]]
|}
|}


== 회귀분석의 종류 ==
==회귀분석의 종류==
* 단순회귀분석: 독립변수 1개
*단순회귀분석: 독립변수 1개
* 다중회귀분석: 독립변수 2개 이상
*다중회귀분석: 독립변수 2개 이상
 
== 장점과 단점 ==
 
* '''장점''': 구현이 간단하며, 해석하기 쉬운 모델이다.
** 과적합 위험이 비교적 낮고, 이진 분류에 효과적이다.
* '''단점''': 선형 관계가 없는 데이터에서는 성능이 떨어진다.
** 다중 클래스 문제에서 직접 적용하기 어려워 소프트맥스 회귀와 같은 다른 기법이 필요합니다.


== 같이 보기 ==
==같이 보기==
* [[회귀 분석]]
*[[회귀 분석]]
* [[선형 회귀]]
*[[선형 회귀]]
[[Category:데이터 과학]]

Latest revision as of 12:49, 31 October 2024

Logistic Regression

로지스틱 회귀는 이진 분류 문제를 해결하는 데 많이 사용되는 통계 및 머신러닝 기법이다. 이 알고리즘은 독립 변수들의 선형 조합을 통해 결과 변수(종속 변수)가 특정 클래스에 속할 확률을 예측한다. 주로 0 또는 1로 레이블된 이진 분류에서 활용되지만, 다중 클래스 확장도 가능하다.

  • 로지스틱: 합격/불합격, 성공/실패, 생존/사망, 진실/거짓 등 이분법적인 결과를 도출하기 위한 경우
  • 회귀분석: 과거의 추세를 기반으로 미래 예측
    • 로지스틱 회귀분석은 종속변수가 범주형이므로, 분류모델에 더 가까움

사용 함수[edit | edit source]

함수 모양
시그모이드

1/(1+e^(-x))

Sigmoid.png

하이퍼볼릭 탄젠트

tanh(x)

Tanh.png

회귀분석의 종류[edit | edit source]

  • 단순회귀분석: 독립변수 1개
  • 다중회귀분석: 독립변수 2개 이상

장점과 단점[edit | edit source]

  • 장점: 구현이 간단하며, 해석하기 쉬운 모델이다.
    • 과적합 위험이 비교적 낮고, 이진 분류에 효과적이다.
  • 단점: 선형 관계가 없는 데이터에서는 성능이 떨어진다.
    • 다중 클래스 문제에서 직접 적용하기 어려워 소프트맥스 회귀와 같은 다른 기법이 필요합니다.

같이 보기[edit | edit source]

Retrieved from "https://itwiki.kr/index.php?title=로지스틱_회귀&oldid=39815"