의사결정 나무: 두 판 사이의 차이
IT 위키
편집 요약 없음 |
잔글 (문자열 찾아 바꾸기 - "분류:데이터 분석" 문자열을 "분류:데이터/통계학" 문자열로) |
||
| 1번째 줄: | 1번째 줄: | ||
[[분류:데이터 | [[분류:데이터/통계학]][[분류:프로젝트 관리]] | ||
;Decision Tree | ;Decision Tree | ||
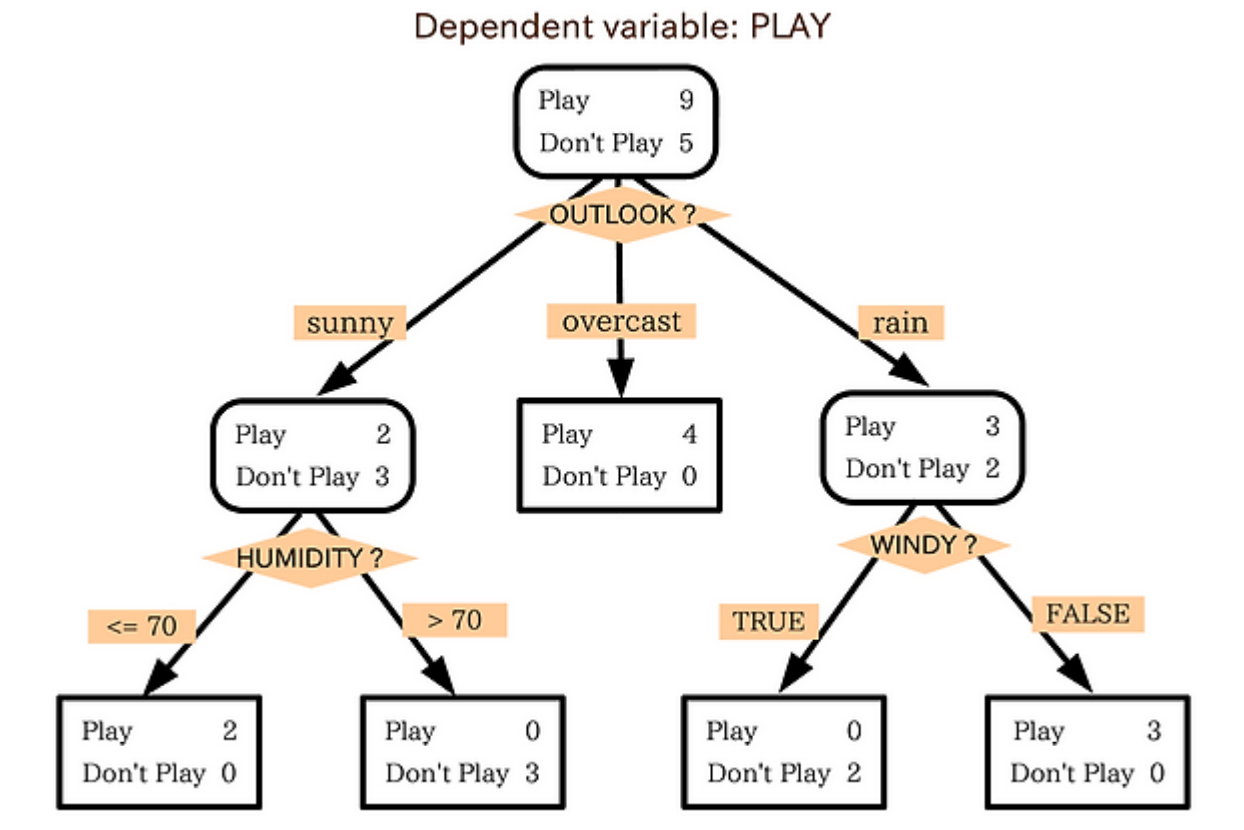
;분류함수를 의사결정 규칙으로 표현할 때 타원(분기점), 직선(가지), 사각형(잎사귀)을 이용하여 나무형태로 그려서 분석하는 기법 | ;분류함수를 의사결정 규칙으로 표현할 때 타원(분기점), 직선(가지), 사각형(잎사귀)을 이용하여 나무형태로 그려서 분석하는 기법 | ||
2020년 3월 8일 (일) 16:17 판
- Decision Tree
- 분류함수를 의사결정 규칙으로 표현할 때 타원(분기점), 직선(가지), 사각형(잎사귀)을 이용하여 나무형태로 그려서 분석하는 기법
유형
| 단계 | 설명 |
|---|---|
| 의사결정 나무 형성 |
분석 목적과 자료구조에 따라 적절하게 분리 기준(Split Criterion) 및 정지규칙(Stopping Rule) 지정 |
| 가지치기 | 분류오류(Classification Error) 유발 위험이 높거나 부적절한 규칙을 가지는 가지(Branch) 제거 |
| 타당성 평가 | 이익 도표(Gains Chart), 위험 도표(Risk Chart), 검정 자료(Test Data)에 의한 교차타당성(Cross Validation) 등을 이용하여 평가 |
| 결과 도출 | 해석 결과에 따라 분류 및 예측 모형 설정 |
활용 알고리즘
| 알고리즘 | 설명 |
|---|---|
| CHAID | 카이제곱 검정(범주형 목표변수) 또는 F-검정(연속형 목표변수)을 이용하여 다지분리(Multiway Split) 수행 |
| CART | 지니 지수(Gini Index, 범주형) 또는 분산의 감소량(연속형)을 이용하여 이진분리(Binary Split) 수행 |
| CS5.0 | 명목형 목표 변수를 지원하는 가장 정확한 알고리즘으로, 다지분리(범주)및 이진분리(수치) 수행 |
장단점
- 장점
- 이해하기 쉬운 모델 형태
- 여러 변수의 영향도 파악 용이
- 계산복잡성 대비 높은 예측 성능
- 분류(classification)와 회귀(regression) 모두 가능
- → 범주나 연속형 수치 모두 예측
- 단점
- 최적해를 보장하지 못함(Greedy 알고리즘)
- 비연속성 분류
- 결정경계(decision boundary)가 데이터 축에 수직인 데이터에만 최적화