리프트 곡선

Lift Curve

리프트 곡선(한국어로 향상 곡선으로도 불린다)은 이진 분류 문제에서 모델의 성능을 평가하는 도구로, 모델이 랜덤 추측에 비해 얼마나 더 나은 결과를 내는지를 시각적으로 보여준다. 특히 불균형 데이터셋에서 모델이 얼마나 잘 예측하는지 측정하는 데 유용하다.

리프트

Lift

모델의 예측이 무작위 예측과 비교하여 얼마나 더 나은지를 표현하는 수치이다. 무작위 예측이 1이라고 가정했을 때 리프트는 배수 값으로 표현된다. 리프트가 1.5라면 무작위 예측보다는 50%의 향상된 성능을 발휘하는 것이다. 정확히 말하면 무작위보다 50% 더 많은 양성 반응을 포함한다.

• 주요 용도는 마케팅 분야로, 고객이나 잠재적인 사용자 반응 예측에 주로 사용된다.
• 특징: 리프트는 낮은 반응률(기저율이 낮은 데이터)인 데이터셋에서 모델의 성능을 측정하는 데 유리하다.
  • 예를 들어, 낮은 클릭률의 예측이나 특정 상품 구매 예측에 적합하다.
• n%의 리프트: 상위 n%에 속하는 예측값을 기준으로 모델의 성능을 측정하는 한다는 의미이다.
  • 모델이 평가한 확률이 가장 높은 n%의 대상으로 평가 했을 때 무작위에 비해 어느 정도 상향을 보이냐는 것이다.
  • 당연히 모델이 평가한 상위 10%는 모델이 가장 확신 있게 판단한 데이터들이므로 양성률이 높을 것이다.
  • 반면 모델이 평가한 상위 50%의 데이터는 무작위 보다는 낫겠지만 상위 10%보단, 무작위 데이터와의 양성률 차이가 작을 것이다.
  • 그리고 100% 리프트 지점에서는 양성률이 전체 데이터와 동일해진다.
    • 아래 그래프를 보면 알 수 있듯이, 100% 지점에서 항상 Random 기준선과 만나게 된다.
    • 예를 들어, 양성 20개와 음성 80개인 데이터(총 100개)가 주어지고, 모델에게 "가장 확신 있는 상위 100개의 양성 데이터를 찾아라"라고 하면, 100개는 전체 데이터와 동일하므로 양성률은 20%로, 무작위 추출 시 양성률과 일치하게 된다.

누적 반응 곡선

Cumulative Response Curves(CRC)

기본 개념 및 예시

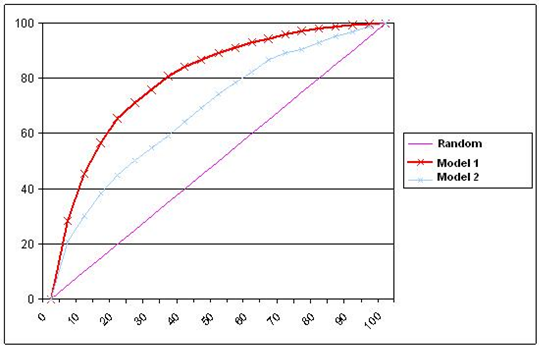
모델이 예측한 각 상위 n%의 데이터별로 실제 양성 포착률이 어떻게 되는지 나타내는 그래프이다. 예를 들면 아래 그래프에서 누적 백분위가 20%일 때 양성 포착율은 60%인데, 이는 누적 백분위가 20%라면 랜덤 추측에서는 20%의 양성 데이터를 포착하겠지만, 이 모델은 60%를 예측했다는 것이다.

• 예를 들어 총 1,000개의 인스턴스 중 양성이 100개가 있다고 가정하자.
• 여기서 랜덤으로 20%를 뽑으면 200개가 뽑히고 그 중에서 양성은 20개가 있다고 추정할 수 있다.
• 그런데 여기서 모델이 가장 확신하는 20%를 뽑으면 마찬가지로 총 200개가 뽑히는데 그 안에 양성이 60개가 있는 것이다.
• 이 경우 리프트는 3이 된다. (기준 비율인 20%의 3배이므로)

• X축 (누적 백분위): 상위부터 하위까지 예측값을 정렬하여 상위 n%씩 누적한 데이터이다.
• Y축 (누적 양성 비율): X축의 상위 n%에 포함된 데이터에서 포착한 양성 반응의 비율을 누적하여 표시한다.

해석

곡선이 가파르게 상승할수록 모델이 초기 단계에서 더 많은 양성 사례를 예측할 수 있음을 의미한다. 이는 상위 몇 퍼센트의 데이터에서 양성 사례를 잘 예측하고 있다는 뜻이다.

대각선과 가까운 곡선은 모델이 랜덤 추측과 거의 다를 바 없는 성능을 보인다는 것을 의미한다. 즉, 이 경우 모델의 성능은 크게 유의미하지 않다고 볼 수 있다.

다른 명칭

• 다른 이름으로, Gain Chart라고 불리기도 한다.
  • 이 그래프를 그냥 "리프트 곡선(Lift Curve)"이라고 부르는 경우도 종종 있다. 리프트를 보기 위한 그래프이기 때문인데 정식 명칭은 CRC 또는 Gain Chart이며. 아래에서 설명하는 것이 진짜 리프트 곡선이다.

리프트 곡선

Lift Curve 섬네일|500x500픽셀

CRC와의 비교

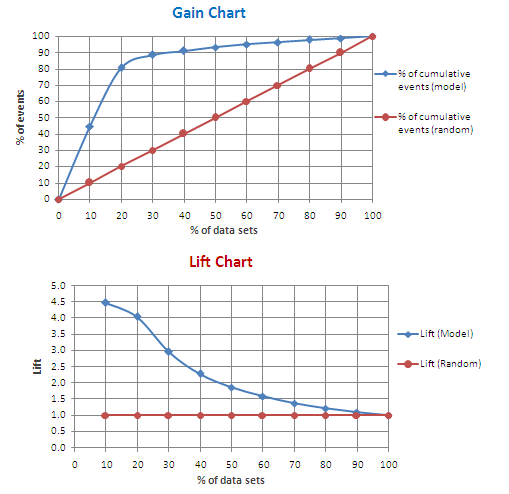
• CRC(Gain Chart)는 모델이 특정 백분위까지 누적된 데이터를 기준으로 얼마나 많은 목표 사례(양성)를 식별하는지를 보여준다. X축이 증가할수록 Y축 값이 더 많은 목표 사례를 포함하게 되어 상승한다.
• 리프트 커브는 특정 백분위에서 모델이 무작위보다 얼마나 더 나은 성능을 발휘하는지를 비율로 나타내며, 리프트 값이 1로 수렴하는 것이 특징이다. 즉 리프트값 자체에 대한 그래프이다.
  • 리프트 커브의 Y축은 리프트 값이다. Gain Chart에서 백분위가 10%일 때 랜덤 예측률이 10%이고, 모델의 예측률은 45%인데, 이 경우 리프트 값이 4.5이다. 아래 리프트 차트(곡선)을 보면 백분위 10%일 때 Y축이 4.5라는 것을 알 수 있다.
  • Gain Chart에서 백분위가 증가함에 따라 Random 기준선과의 차이가 줄어들어 결국 만나는 것과 같이 Lift Curve에선 항상 결국 1로 수렴하게 된다.

해석

• 리프트 차트는 백분위별 모델의 성능 향상률(무작위 대비)을 직관적으로 알 수 있다. 리프트가 수치로 바로 보여지기 때문이다. 그래서 초기 값이 높은 것이 좋으며, 그래프가 급격하게 떨어지면 상대적으로 확신한 값의 상위 순위가 적중률이 높다는 것이다.
• 따라서 이 그래프는 마케팅에서 고객 1%를 타겟으로 할 것인지 5%를 타겟으로 할 것인지와 같이 상대적으로 높게 확신할 수 있는 비율을 판별하기에 매우 유리하다. 지금 좌측의 그래프는 예시라 비교적 완만한 편이지만, 실제 기저율이 낮은 데이터는 그래프가 훨씬 급하게 떨어지므로, 급격하게 떨어지기 직전까지의 백분위기 강하게 확신해볼 수 있는 범위인 것이다.