ROC 곡선: Difference between revisions
No edit summary |
No edit summary |
||
| Line 23: | Line 23: | ||
* '''y축''': True Positive Rate(TPR) | * '''y축''': True Positive Rate(TPR) | ||
** = Sensitivity, Recall | ** = Sensitivity, Recall | ||
여기서 임계값(Threshold 또는 cuf-off)는 그래프의 축에 없는데, 일반적으로 ROC 곡선을 따라서 올라가며 감소하는 경향을 보인다. 즉 일반적으로 TPR, FPR이 모두 0인 지점에 가까우면(그래프의 왼쪽 아래) 임계값이 높고, TPR, FPR이 모두 1인 지점에 가까우면 임계값이 낮다. 중간에 볼록 솟은 부분이 임계값이 가장 적당한 중간 지점(예를들어 0.5~0.6)이라고 할 수 있다. | |||
임계값이 1에 가까워질수록 모델은 대부분의 샘플을 음성으로 예측할 것이다. 예를 들어 100%의 확률을 임계값으로 한다면 양성으로 예측할 모델이 거의 없다. 99%도 마찬가지다. 90% 이상의 정확도를 요구해도 상당히 낮은 비율만 양성으로 예측할 것이다. 다만 이런 기춘치가 80, 70으로 내려갈 수록 양성 예측률이 높아진다. | 임계값이 1에 가까워질수록 모델은 대부분의 샘플을 음성으로 예측할 것이다. 예를 들어 100%의 확률을 임계값으로 한다면 양성으로 예측할 모델이 거의 없다. 99%도 마찬가지다. 90% 이상의 정확도를 요구해도 상당히 낮은 비율만 양성으로 예측할 것이다. 다만 이런 기춘치가 80, 70으로 내려갈 수록 양성 예측률이 높아진다. | ||
| Line 28: | Line 29: | ||
그리고 임계값이 0에 가까워질수록 대부분의 샘플을 양성으로 예측하게 된다. ROC 곡선은 임계값이 변화할 때 모델의 성능이 어떻게 변화하는지 보여준다. | 그리고 임계값이 0에 가까워질수록 대부분의 샘플을 양성으로 예측하게 된다. ROC 곡선은 임계값이 변화할 때 모델의 성능이 어떻게 변화하는지 보여준다. | ||
== | == ROC 그리기 예시 == | ||
사람이 직접 하나하나 계산해서 그리는 것은 거의 불가능하다. 일반적으론 도구를 이용해서 그린다. 다만 간단하게 나마 그려 봐야 이해가 쉽기 때문에 적은 수의 데이터로 그리는 걸 시도해볼 수 있다. | |||
{| class="wikitable" | {| class="wikitable" | ||
!'''실제 값 (정답)''' | !'''실제 값 (정답)''' | ||
| Line 57: | Line 59: | ||
|0.1 | |0.1 | ||
|} | |} | ||
위 데이터는 예측 확률 0.6~0.7을 기점으로 그 이하는 모두 실제로 음성, 그 이상은 실제로 모두 양성이라는 측면에서 ROC 커브를 쉽게 예상할 수 있다. 아래 AUC 파트의 "이론적으로 완벽한 모델의 ROC(AUC=1)" 그래프와 동일한 모양이 될 것이다. 실제로 계산을 해보자. | |||
'''임계값 변화에 따른 예측 결과:''' | '''임계값 변화에 따른 예측 결과:''' | ||
| Line 74: | Line 78: | ||
이 데이터들을 바탕으로 각각의 임계값에서 True Positive Rate (TPR)와 False Positive Rate (FPR)을 계산해 '''ROC 곡선'''을 그린다. | 이 데이터들을 바탕으로 각각의 임계값에서 True Positive Rate (TPR)와 False Positive Rate (FPR)을 계산해 '''ROC 곡선'''을 그린다. | ||
{| class="wikitable" | |||
!Threshold | |||
!FPR | |||
!TPR | |||
|- | |||
|0 | |||
|1 | |||
|1 | |||
|- | |||
|0.1 | |||
|1 | |||
|1 | |||
|- | |||
|0.2 | |||
|0.75 | |||
|1 | |||
|- | |||
|0.3 | |||
|0.25 | |||
|1 | |||
|- | |||
|0.4 | |||
|0.25 | |||
|1 | |||
|- | |||
|0.5 | |||
|0.25 | |||
|1 | |||
|- | |||
|0.6 | |||
|0 | |||
|1 | |||
|- | |||
|0.7 | |||
|0 | |||
|0.75 | |||
|- | |||
|0.8 | |||
|0 | |||
|0.75 | |||
|- | |||
|0.9 | |||
|0 | |||
|0.25 | |||
|- | |||
|1 | |||
|0 | |||
|0 | |||
|} | |||
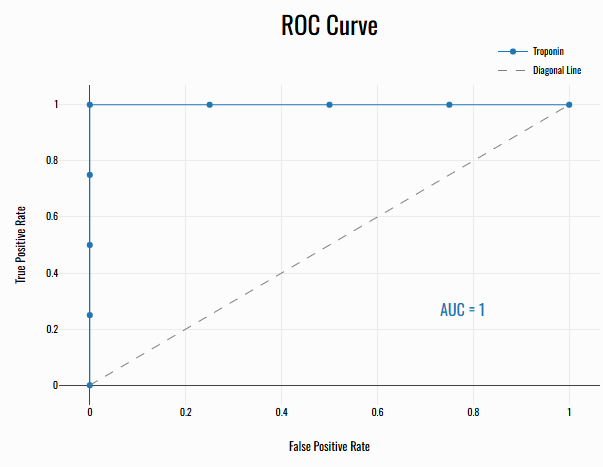
위에서 예측하였듯이 이 사례에선 모든 임계값에서 FPR이 0이거나 TPR이 1이다. 이는, 그래프가 곡선이 아니라 양면에 붙어 있다는 뜻이다. 아래와 같다. | |||
[[파일:ROC 그래프 그리기 예시.png|400x400픽셀]] | |||
이는 현실적으론 나오기 힘든 그래프이다. 특정 확률 이상으로 예측하는 것은 100% 실제 측정값과 동일할 것이라는 의미가 되기 때문이다. 일반적으론 아래와 같이 모델이 예측력이 완벽하지 않은 상태에서 이를 평가하기 위해 사용된다. 아래 데이터를 보자. | |||
{| class="wikitable" | |||
!'''실제 값 (정답)''' | |||
!'''모델의 예측 확률 (양성일 확률)''' | |||
|- | |||
|양성 (1) | |||
|0.95 | |||
|- | |||
|양성 (1) | |||
|0.6 | |||
|- | |||
|양성 (1) | |||
|0.8 | |||
|- | |||
|음성 (0) | |||
|0.3 | |||
|- | |||
|음성 (0) | |||
|0.2 | |||
|- | |||
|음성 (0) | |||
|0.7 | |||
|- | |||
|양성 (1) | |||
|0.85 | |||
|- | |||
|음성 (0) | |||
|0.1 | |||
|}이번엔 모델의 예측 확률이 0.6인 것이 실제로는 양성이었는데, 모델의 예측 확률이 0.7인 것이 실제로는 음성이었다. 예측에 실패한 것이다. 이때 임계치 별 FPR, TPR을 계산해보면 아래와 같다. | |||
{| class="wikitable" | |||
!Threshold | |||
!FPR | |||
!TPR | |||
|- | |||
|0 | |||
|1 | |||
|1 | |||
|- | |||
|0.1 | |||
|1 | |||
|1 | |||
|- | |||
|0.2 | |||
|0.75 | |||
|1 | |||
|- | |||
|0.3 | |||
|0.25 | |||
|1 | |||
|- | |||
|0.4 | |||
|0.25 | |||
|1 | |||
|- | |||
|0.5 | |||
|0.25 | |||
|1 | |||
|- | |||
|0.6 | |||
|0.25 | |||
|0.75 | |||
|- | |||
|0.7 | |||
|0 | |||
|0.75 | |||
|- | |||
|0.8 | |||
|0 | |||
|0.75 | |||
|- | |||
|0.9 | |||
|0 | |||
|0.25 | |||
|- | |||
|1 | |||
|0 | |||
|0 | |||
|} | |||
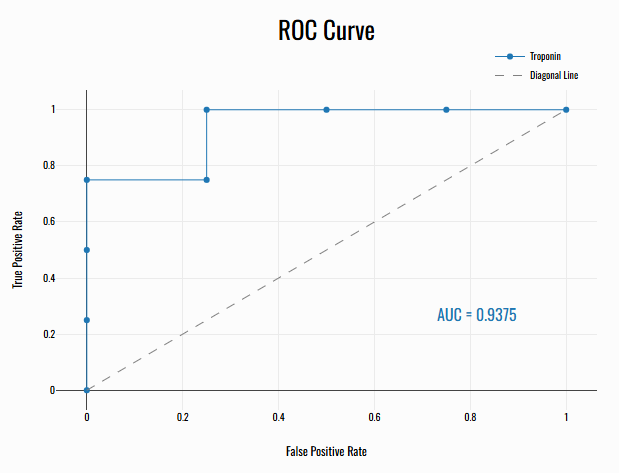
위 표를 보면 0.6에서 FPR이 0이 아니면서 TPR이 1이 아닌 경우가 발생했다. 이렇게 자연스럽게 특정 임계 범위에서 예측에 실패하는 경우가 있어야 그래프가 우리가 일반적으로 보는 볼록한 형태에 가까워진다. (물론 이 사례는 너무 데이터가 작아 볼록하게 보이진 않을 것이다.) | |||
여기서 그래프에 임계값이 표시되지 않지만 우리는 저기 볼록 들어간 지점이 임계값 0.6 지점이라는 것을 알 수 있다. | |||
[[파일:ROC 그래프 그리기 예시2.png|400x400픽셀]] | |||
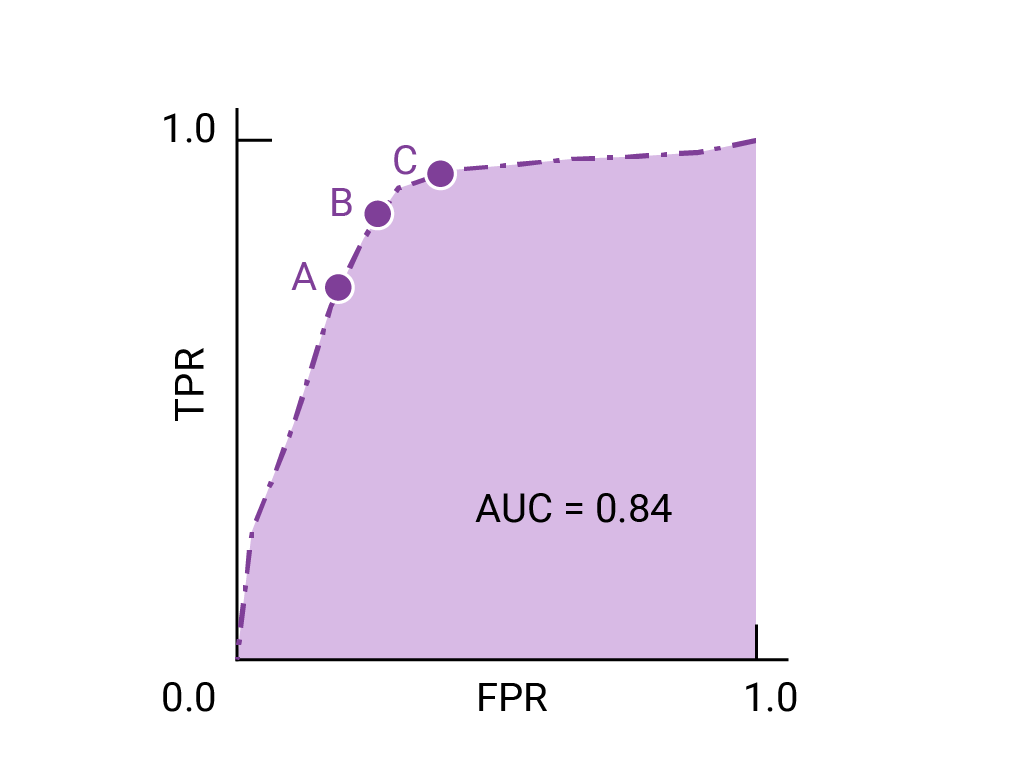
== 최적의 임계치 선택 == | |||
[[파일:ROC를 통한 임계값 선택.png|360x360픽셀]] | [[파일:ROC를 통한 임계값 선택.png|360x360픽셀]] | ||
Latest revision as of 01:51, 31 October 2024
Receiver Operating Characteristic; Receiver Operating Characteristic Curve
ROC 곡선은 분류 모델의 성능을 평가하는데 사용되는 도구로, 주로 이진 분류 문제에서 모델이 얼마나 잘 분류하는지 시각적으로 보여준다. ROC 곡선은 다양한 임계값에서 모델의 민감도(양성 탐지율)와 거짓 양성 비율 간의 관계를 나타낸다.
ROC 곡선의 구성 요소[edit | edit source]
- 민감도: 실제 양성인 샘플 중에서 모델이 올바르게 양성으로 예측한 비율이다.
- TPR = TP / TP + FN
- TP(True Positive): 실제로 양성인 경우를 양성으로 예측한 경우
- FN(False Negative): 실제로 양성인 경우를 음성으로 예측한 경우
- False Positive Rate (FPR): 실제로 음성인 샘플 중에서 모델이 잘못 양성으로 예측한 비율
- 거짓 양성 비율 (1 - 특이도): 실제 음성인 샘플 중에서 양성으로 잘못 예측한 비율이다.
- FPR = FP / (FP + TN)
- FP(False Positive): 실제로 음성인 경우를 양성으로 예측한 경우
- TN(True Negative): 실제로 음성인 경우를 음성으로 예측한 경우
ROC 곡선 그리기[edit | edit source]
 ROC 곡선은 모델의 임계값(Threshold)을 조정하면서 True Positive Rate와 False Positive Rate의 변화를 시각화한다. 임계값을 다르게 설정함에 따라 모델의 성능이 달라지기 때문에, 여러 임계값에서 TPR과 FPR을 계산하여 그래프를 그린다.
ROC 곡선은 모델의 임계값(Threshold)을 조정하면서 True Positive Rate와 False Positive Rate의 변화를 시각화한다. 임계값을 다르게 설정함에 따라 모델의 성능이 달라지기 때문에, 여러 임계값에서 TPR과 FPR을 계산하여 그래프를 그린다.
- x축: False Positive Rate(FPR)
- = 1 - Specificity
- y축: True Positive Rate(TPR)
- = Sensitivity, Recall
여기서 임계값(Threshold 또는 cuf-off)는 그래프의 축에 없는데, 일반적으로 ROC 곡선을 따라서 올라가며 감소하는 경향을 보인다. 즉 일반적으로 TPR, FPR이 모두 0인 지점에 가까우면(그래프의 왼쪽 아래) 임계값이 높고, TPR, FPR이 모두 1인 지점에 가까우면 임계값이 낮다. 중간에 볼록 솟은 부분이 임계값이 가장 적당한 중간 지점(예를들어 0.5~0.6)이라고 할 수 있다.
임계값이 1에 가까워질수록 모델은 대부분의 샘플을 음성으로 예측할 것이다. 예를 들어 100%의 확률을 임계값으로 한다면 양성으로 예측할 모델이 거의 없다. 99%도 마찬가지다. 90% 이상의 정확도를 요구해도 상당히 낮은 비율만 양성으로 예측할 것이다. 다만 이런 기춘치가 80, 70으로 내려갈 수록 양성 예측률이 높아진다.
그리고 임계값이 0에 가까워질수록 대부분의 샘플을 양성으로 예측하게 된다. ROC 곡선은 임계값이 변화할 때 모델의 성능이 어떻게 변화하는지 보여준다.
ROC 그리기 예시[edit | edit source]
사람이 직접 하나하나 계산해서 그리는 것은 거의 불가능하다. 일반적으론 도구를 이용해서 그린다. 다만 간단하게 나마 그려 봐야 이해가 쉽기 때문에 적은 수의 데이터로 그리는 걸 시도해볼 수 있다.
| 실제 값 (정답) | 모델의 예측 확률 (양성일 확률) |
|---|---|
| 양성 (1) | 0.95 |
| 음성 (0) | 0.6 |
| 양성 (1) | 0.8 |
| 음성 (0) | 0.3 |
| 음성 (0) | 0.2 |
| 양성 (1) | 0.7 |
| 양성 (1) | 0.85 |
| 음성 (0) | 0.1 |
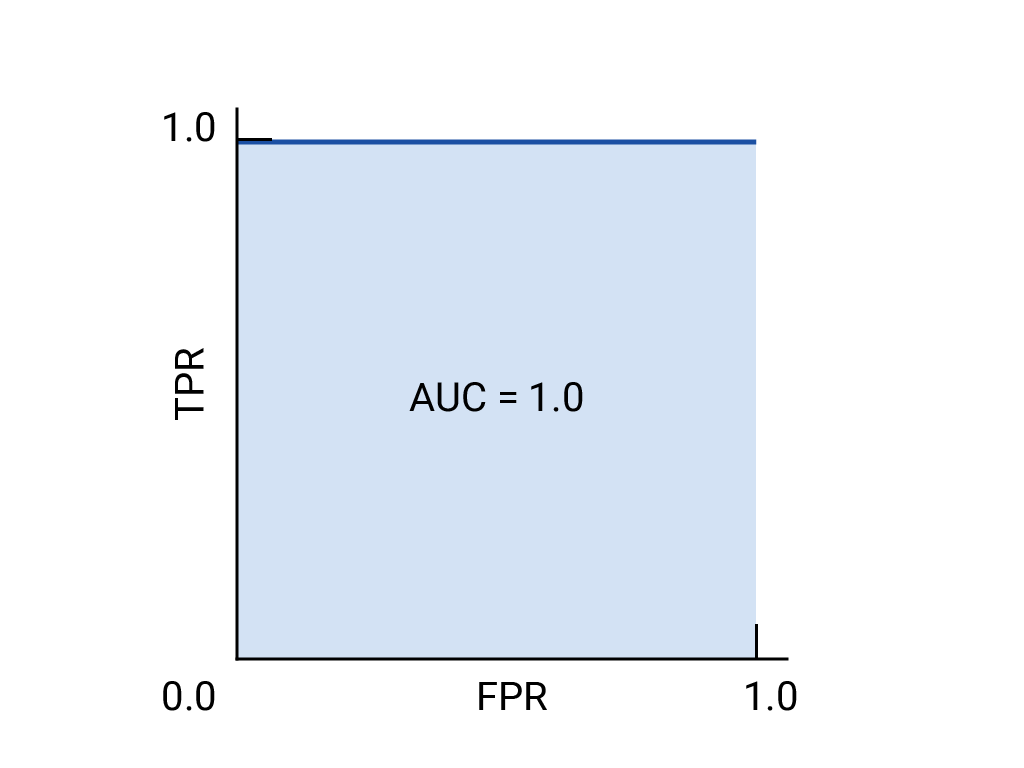
위 데이터는 예측 확률 0.6~0.7을 기점으로 그 이하는 모두 실제로 음성, 그 이상은 실제로 모두 양성이라는 측면에서 ROC 커브를 쉽게 예상할 수 있다. 아래 AUC 파트의 "이론적으로 완벽한 모델의 ROC(AUC=1)" 그래프와 동일한 모양이 될 것이다. 실제로 계산을 해보자.
임계값 변화에 따른 예측 결과:
- 임계값이 0.9일 때:
- 예측 확률이 0.9 이상인 경우만 양성으로 예측.
- 이 경우, 0.95에 해당하는 첫 번째 샘플만 양성으로 예측되고 나머지는 모두 음성으로 예측됨.
- True Positive (TP): 1건, False Positive (FP): 0건, False Negative (FN): 3건, True Negative (TN): 4건.
- 임계값이 0.5일 때:
- 예측 확률이 0.5 이상이면 양성으로 예측.
- 이 경우, 0.60, 0.80, 0.70, 0.85를 가진 샘플도 양성으로 예측.
- TP: 4건, FP: 1건, FN: 0건, TN: 3건.
- 임계값이 0.1일 때:
- 거의 모든 샘플이 양성으로 예측됨. (예측 확률이 0.1보다 크므로 대부분 양성으로 분류됨)
- TP: 4건, FP: 3건, FN: 0건, TN: 0건.
ROC 곡선 그리기:
이 데이터들을 바탕으로 각각의 임계값에서 True Positive Rate (TPR)와 False Positive Rate (FPR)을 계산해 ROC 곡선을 그린다.
| Threshold | FPR | TPR |
|---|---|---|
| 0 | 1 | 1 |
| 0.1 | 1 | 1 |
| 0.2 | 0.75 | 1 |
| 0.3 | 0.25 | 1 |
| 0.4 | 0.25 | 1 |
| 0.5 | 0.25 | 1 |
| 0.6 | 0 | 1 |
| 0.7 | 0 | 0.75 |
| 0.8 | 0 | 0.75 |
| 0.9 | 0 | 0.25 |
| 1 | 0 | 0 |
위에서 예측하였듯이 이 사례에선 모든 임계값에서 FPR이 0이거나 TPR이 1이다. 이는, 그래프가 곡선이 아니라 양면에 붙어 있다는 뜻이다. 아래와 같다.
이는 현실적으론 나오기 힘든 그래프이다. 특정 확률 이상으로 예측하는 것은 100% 실제 측정값과 동일할 것이라는 의미가 되기 때문이다. 일반적으론 아래와 같이 모델이 예측력이 완벽하지 않은 상태에서 이를 평가하기 위해 사용된다. 아래 데이터를 보자.
| 실제 값 (정답) | 모델의 예측 확률 (양성일 확률) |
|---|---|
| 양성 (1) | 0.95 |
| 양성 (1) | 0.6 |
| 양성 (1) | 0.8 |
| 음성 (0) | 0.3 |
| 음성 (0) | 0.2 |
| 음성 (0) | 0.7 |
| 양성 (1) | 0.85 |
| 음성 (0) | 0.1 |
이번엔 모델의 예측 확률이 0.6인 것이 실제로는 양성이었는데, 모델의 예측 확률이 0.7인 것이 실제로는 음성이었다. 예측에 실패한 것이다. 이때 임계치 별 FPR, TPR을 계산해보면 아래와 같다.
| Threshold | FPR | TPR |
|---|---|---|
| 0 | 1 | 1 |
| 0.1 | 1 | 1 |
| 0.2 | 0.75 | 1 |
| 0.3 | 0.25 | 1 |
| 0.4 | 0.25 | 1 |
| 0.5 | 0.25 | 1 |
| 0.6 | 0.25 | 0.75 |
| 0.7 | 0 | 0.75 |
| 0.8 | 0 | 0.75 |
| 0.9 | 0 | 0.25 |
| 1 | 0 | 0 |
위 표를 보면 0.6에서 FPR이 0이 아니면서 TPR이 1이 아닌 경우가 발생했다. 이렇게 자연스럽게 특정 임계 범위에서 예측에 실패하는 경우가 있어야 그래프가 우리가 일반적으로 보는 볼록한 형태에 가까워진다. (물론 이 사례는 너무 데이터가 작아 볼록하게 보이진 않을 것이다.)
여기서 그래프에 임계값이 표시되지 않지만 우리는 저기 볼록 들어간 지점이 임계값 0.6 지점이라는 것을 알 수 있다.
최적의 임계치 선택[edit | edit source]
위와 같은 그래프가 나왔을 때
- 거짓 양성이 나왔을 때 비용이 많이 드는 경우, TPR이 다소 낮더라도 A 지점에서처럼 더 낮은 FPR을 제공하는 임곗값을 선택한다.
- 반대로 거짓 양성이 비용이 적게 들고 거짓 음성이 비용이 많이 든다면 포인트 C의 임곗값을 선택하여 TPR을 최대화하는 것이 바람직할 수 있다.
- 비용이 거의 동일하다면 B 포인트가 가장 적합하다. 이와 같이 그래프를 통해 TPR과 FPR 사이의 최적의 균형을 취할 수 있다.
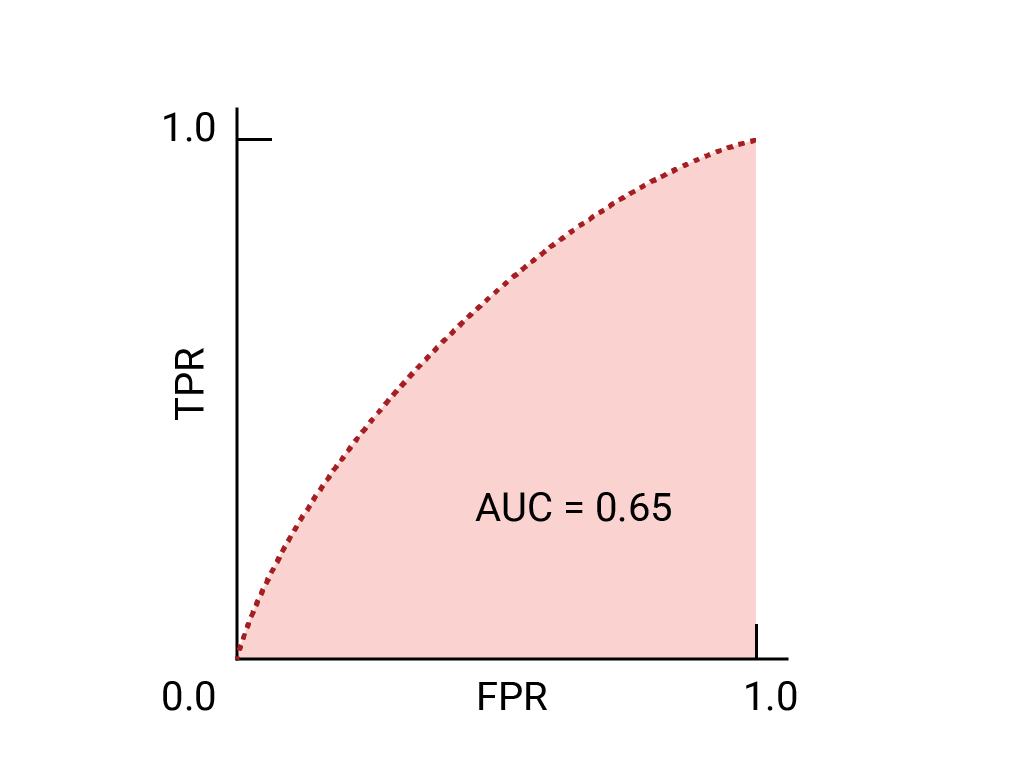
AUC[edit | edit source]
ROC 곡선 아래의 면적인 AUC(Area Under the Curve)는 모델의 분류 성능을 수치화한 값으로, 0과 1 사이의 값을 가진다. AUC 값은 다음과 같이 해석할 수 있다:
- AUC = 1: 완벽한 분류 모델
- AUC = 0.5: 무작위 추측과 동일한 성능
- AUC < 0.5: 성능이 무작위 추측보다 나쁨
일반적으로, AUC 값이 0.7 이상이면 모델이 좋은 성능을 가진다고 평가한다.
ROC 곡선이 유용한 이유[edit | edit source]
ROC 곡선은 모델의 성능을 임계값의 변화에 따라 시각적으로 보여주기 때문에, 분류 임계값을 설정하는 데 중요한 정보를 제공한다. 특히, 클래스가 불균형한 데이터셋에서도 성능을 평가할 수 있는 장점이 있다. Precision-Recall 곡선과 함께 사용하면 모델의 성능을 더욱 정확하게 분석할 수 있다.