스킵 리스트

스킵 리스트(skip list)는 정렬된 원소를 빠르게 탐색, 삽입, 삭제할 수 있도록 설계된 확률적 자료구조이다. 1989년 William Pugh가 제안하였으며, 연결 리스트(linked list)의 구조를 확장하여 이진 탐색 트리 수준의 효율성을 얻을 수 있도록 고안되었다.

1 개요

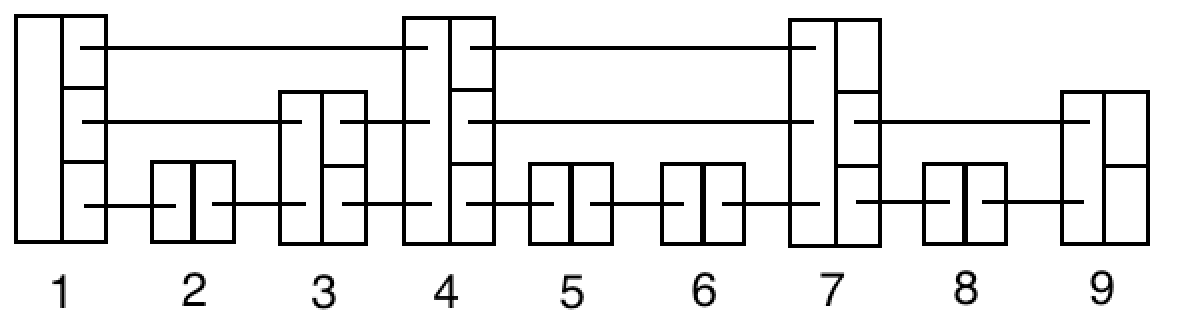
스킵 리스트는 여러 수준의 연결 리스트를 위로 확장한 구조를 가진다. 기본 연결 리스트는 가장 하위 레벨에 존재하며, 그 위로 확률적으로 선택된 노드들만 포함하는 상위 레벨들이 존재한다. 각 노드는 자신이 속한 레벨의 다음 노드를 가리키는 포인터를 가진다. 탐색, 삽입, 삭제 등의 연산은 상위 레벨부터 내려가며 진행되어, 일반 연결 리스트보다 빠른 속도를 제공한다.

2 구조

스킵 리스트는 레벨(level)의 개념을 기반으로 구성된다.

• Level 0: 전체 원소를 포함하는 기본 연결 리스트
• Level 1 이상: 일정 확률(p, 일반적으로 1/2 또는 1/4)에 따라 무작위로 선택된 노드만 포함
• Head node: 모든 레벨의 시작점을 포함하는 특수 노드

노드마다 여러 개의 포인터가 있으며, 자신의 레벨 수에 따라 상위 레벨까지 연결된다.

3 연산

스킵 리스트는 다음과 같은 주요 연산을 효율적으로 수행할 수 있도록 설계되었다.

• 탐색
  • 탐색 연산은 찾고자 하는 키 값 k에 대해, 가장 높은 레벨에서 시작하여 오른쪽으로 이동하면서 현재 노드의 다음 노드의 키가 k 이하일 때까지 진행한다.
  • 조건이 만족되지 않으면 한 단계 아래 레벨로 내려가 같은 과정을 반복하며, 최하위 레벨까지 도달한 후 k 이하의 가장 큰 키 값을 갖는 노드를 찾는다.

• 삽입
  • 삽입할 위치는 탐색 연산을 통해 찾는다. 그 후, 새 노드의 레벨을 확률적으로 결정하여 해당 레벨까지의 포인터를 조정한다.
  • 새 노드는 0번 레벨(가장 아래)부터 자신의 레벨까지의 모든 레벨에서 연결되어야 하며, 각 레벨마다 이전 노드의 포인터를 적절히 갱신해야 한다.
  • 레벨이 기존 최대 레벨보다 높아지면, 리스트의 레벨도 확장된다.

• 삭제
  • 삭제 연산도 먼저 탐색을 통해 삭제 대상 노드를 찾는다.
  • 이후 해당 노드가 존재하는 각 레벨에서 연결 포인터를 수정하여 노드를 제거한다.
  • 삭제 이후 상위 레벨에서 더 이상 노드가 없다면 리스트의 전체 레벨을 줄이는 작업이 수행된다.

4 시간 복잡도

스킵 리스트는 다음과 같은 평균 시간 복잡도를 갖는다.

• 탐색: O(log n)
• 삽입: O(log n)
• 삭제: O(log n)

최악의 경우 O(n)일 수 있으나, 확률적 구조 덕분에 평균적으로는 균형잡힌 이진 탐색 트리와 유사한 성능을 가진다.

아래 분석 내용은 일부 p = 1/2으로 고정하여 쓰여졌음에 주의하자.

4.1 탐색

• 최상위 레벨에서 시작하여 다음 규칙에 따라 탐색한다.
  • 현재 노드의 다음(next) 노드의 키가 찾고자 하는 키보다 작으면 → 오른쪽으로 이동
  • 그 외의 경우 → 한 단계 아래 레벨로 내려감
• 레벨 0까지 반복하면서, 마지막으로 지나간 노드를 반환한다.
• 탐색은 각 레벨당 평균 한 번씩 이동하므로, 전체 기대 시간은 O(log n)이다.

4.2 삽입

• 새 노드의 레벨은 확률 p 에 따라 무작위로 결정된다.
  • 레벨 k가 선택될 확률은 p^(k+1), 예를 들어 p=1/2이면 (1/2)^(k+1)
• 삽입 위치 찾기 (검색 단계)
  • 탐색과 동일하게 최고 레벨부터 오른쪽으로 이동하고, 조건이 맞지 않으면 아래로 내려가며 레벨 0까지 반복
  • 각 레벨에서 새 노드가 삽입될 위치의 직전 노드를 기록
  • 이 탐색 단계의 기대 시간은 O(log n)
• 포인터 갱신 (삽입 단계)
  • 선택된 최고 레벨 h에 대해, 각 레벨 i (0 ≤ i ≤ h)에 대해 다음을 수행***새 노드의 next[i]를 prev[i].next[i]로 지정
    • prev[i].next[i]를 새 노드로 갱신
  • 레벨 h의 기대값은 상수 수준이므로, 이 단계의 기대 시간은 O(1)
• 삽입 전체 기대 시간: O(log n)

4.3 삭제

• 삭제할 노드의 위치를 탐색하는 과정은 삽입 시와 동일하게 수행된다.
  • 최상위 레벨에서 시작하여, 각 레벨에서 삭제 대상 노드 직전까지 이동
  • 레벨 0에서 삭제할 노드를 확인
  • 이 탐색 단계의 기대 시간은 O(log n)
• 포인터 갱신 (삭제 단계)
  • 삭제할 노드가 레벨 h에 존재한다고 할 때, 각 레벨 i (0 ≤ i ≤ h)에 대해
    • prev[i].next[i]를 삭제 노드의 next[i]로 갱신
  • 레벨 h의 기대값은 상수 수준이므로, 이 단계의 기대 시간은 O(1)
• 삭제 전체 기대 시간: O(log n)

5 공간 복잡도

• 각 키가 레벨 k를 갖는 확률은 1/2^(k+1)
• 따라서 레벨 k에 속하는 노드 수의 기대값은 n × 1/2^(k+1)
• 모든 레벨을 더하면
  • n×(1/2 + 1/4 + 1/8 + …) = n
• 결국 원래 리스트와 상위 레벨들을 합하면 2n이다. 따라서 선형 복잡도 수준이므로,
• 결론: 기대 공간 복잡도는 O(n)입니다.

6 예제

다음은 Python으로 구현한 스킵 리스트의 주요 연산(탐색, 삽입, 삭제) 예시이다.

import random

class SkipNode:
    def __init__(self, key, level):
        self.key = key
        self.forward = [None] * (level + 1)

class SkipList:
    def __init__(self, max_level, p):
        self.max_level = max_level  # 최대 레벨
        self.p = p                  # 노드가 상위 레벨에 포함될 확률
        self.header = SkipNode(float('-inf'), max_level)
        self.level = 0             # 현재 리스트의 최대 레벨

    def random_level(self):
        lvl = 0
        while random.random() < self.p and lvl < self.max_level:
            lvl += 1
        return lvl

    def look_up(self, key):
        u = self.header
        for i in reversed(range(self.level + 1)):
            while u.forward[i] and u.forward[i].key <= key:
                u = u.forward[i]
        return u  # key 이하의 가장 큰 노드 반환

    def search(self, key):
        node = self.look_up(key)
        return node if node.key == key else None

    def insert(self, key):
        update = [None] * (self.max_level + 1)
        u = self.header
        for i in reversed(range(self.level + 1)):
            while u.forward[i] and u.forward[i].key < key:
                u = u.forward[i]
            update[i] = u

        node = u.forward[0]
        if node and node.key == key:
            return  # 중복 키는 삽입하지 않음

        lvl = self.random_level()
        if lvl > self.level:
            for i in range(self.level + 1, lvl + 1):
                update[i] = self.header
            self.level = lvl

        new_node = SkipNode(key, lvl)
        for i in range(lvl + 1):
            new_node.forward[i] = update[i].forward[i]
            update[i].forward[i] = new_node

    def delete(self, key):
        update = [None] * (self.max_level + 1)
        u = self.header
        for i in reversed(range(self.level + 1)):
            while u.forward[i] and u.forward[i].key < key:
                u = u.forward[i]
            update[i] = u

        node = u.forward[0]
        if node and node.key == key:
            for i in range(self.level + 1):
                if update[i].forward[i] != node:
                    continue
                update[i].forward[i] = node.forward[i]

            while self.level > 0 and self.header.forward[self.level] is None:
                self.level -= 1

# 실행 예시
if __name__ == "__main__":
    sl = SkipList(max_level=4, p=0.5)
    for k in [3, 6, 7, 9, 12, 19]:
        sl.insert(k)

    print("Search 6:", sl.search(6).key if sl.search(6) else "Not Found")
    sl.delete(6)
    print("Search 6 after deletion:", sl.search(6).key if sl.search(6) else "Not Found")

자료 구조 위 구현은 다음과 같은 구조를 따른다.

• 각 노드는 key 값을 가지며, 최대 max_level+1 개의 forward 포인터를 가진다.
• SkipList는 확률 p를 기준으로 랜덤하게 레벨을 결정하고, 삽입 시 각 레벨에 노드를 연결한다.
• look_up 연산은 상위 레벨부터 오른쪽으로 이동하며 key 이하의 가장 큰 노드를 찾아 반환한다.

7 장점

• 간단한 구현으로도 이진 탐색 트리 수준의 성능 달성
• 포인터 조작만으로 동적 삽입, 삭제에 용이
• 동시성 제어가 상대적으로 쉬움 (Lock-free skip list 구현 등)

8 단점

• 공간 사용량 증가 (다수의 포인터 필요)
• 성능이 확률에 의존함

9 같이 보기

• 이진 탐색 트리
• 연결 리스트
• 해시 테이블
• AVL 트리
• 동시성 제어

10 참고 문헌

• William Pugh (1990). "Skip Lists: A Probabilistic Alternative to Balanced Trees". Communications of the ACM.
• Cormen, T. H., Leiserson, C. E., Rivest, R. L., and Stein, C. (2009). Introduction to Algorithms. MIT Press.