트리: 두 판 사이의 차이
IT 위키
편집 요약 없음 |
AlanTuring (토론 | 기여) 편집 요약 없음 |
||
| (사용자 2명의 중간 판 2개는 보이지 않습니다) | |||
| 1번째 줄: | 1번째 줄: | ||
[[분류:자료 구조]] | [[분류:자료 구조]] | ||
Tree | |||
트리(Tree)는 계층적 구조를 가지는 비선형 자료 구조로, 하나의 루트 노드(Root Node)에서 시작하여 여러 개의 자식 노드를 가질 수 있다. 트리는 그래프의 한 종류이며, 방향성이 있는 비순환 그래프(DAG, Directed Acyclic Graph)로 볼 수 있다. | |||
*[[비선형 구조|비선형]], [[비순환 구조]] | |||
== 관련 용어 == | ==트리의 특성== | ||
*트리는 노드와 간선으로 구성된다. | |||
*순환(Cycle)이 존재하지 않는다. | |||
*n개의 노드를 가진 트리는 항상 (n-1)개의 간선을 가진다. | |||
*루트에서 특정 노드까지의 경로는 유일하다. | |||
==관련 용어== | |||
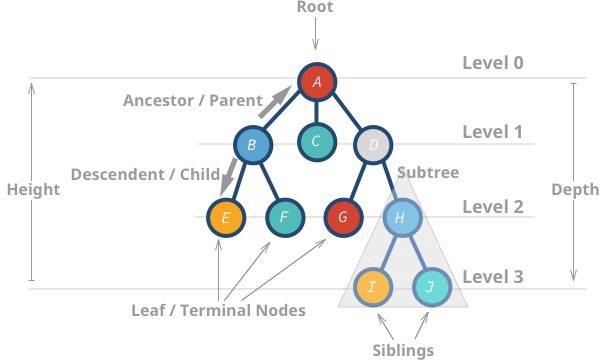
[[파일:트리 용어.jpeg]] | [[파일:트리 용어.jpeg]] | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
! 용어 !! 의미 | !용어!!의미 | ||
|- | |- | ||
| 차수(degree) || 노드의 부족 트리의 개수 | |차수(degree)|| 노드의 부족 트리의 개수 | ||
* 트리 전체의 차수: 트리에 속한 최대 차수 | *트리 전체의 차수: 트리에 속한 최대 차수 | ||
|- | |- | ||
| 단말 노드(leaf, terminal) || 차수가 0인, 가장 끝의 노드 | |단말 노드(leaf, terminal)|| 차수가 0인, 가장 끝의 노드 | ||
|- | |- | ||
| 내부 노드(internal) || 차수가 1 이상인, 단말이 아닌 노드 | |내부 노드(internal)||차수가 1 이상인, 단말이 아닌 노드 | ||
|- | |- | ||
| 부모(parent) || 바로 상위 노드 | |부모(parent)||바로 상위 노드 | ||
|- | |- | ||
| 자식(child) || 바로 하위 노드 | | 자식(child)||바로 하위 노드 | ||
|- | |- | ||
| 형제(sibling) || 부모가 같은 노드 | |형제(sibling)||부모가 같은 노드 | ||
|- | |- | ||
| 조상(ancestor) || 상위 노드, 부모 노드들의 집합 | |조상(ancestor)||상위 노드, 부모 노드들의 집합 | ||
|- | |- | ||
| 자손(descendant) || 하위 노드, 자식 노드들의 집합 | |자손(descendant) ||하위 노드, 자식 노드들의 집합 | ||
|- | |- | ||
| 레벨(level) || 상위 노드를 기준으로 한 깊이 | |레벨(level)||상위 노드를 기준으로 한 깊이 | ||
|- | |- | ||
| 깊이(depth) || 트리에 속한 최대 레벨 | |깊이(depth)||트리에 속한 최대 레벨 | ||
|} | |} | ||
== 트리의 활용 == | '''예시''' | ||
* 검색: log(n)의 효율 | <syntaxhighlight lang="plaintext"> | ||
* 인덱스: [[B 트리]], [[AVL 트리]], [[T 트리]] 등 | A → 루트 노드 (깊이 0) | ||
* | / \ | ||
B C → 깊이 1 | |||
/ \ \ | |||
D E F → 깊이 2 (리프 노드: D, E, F) | |||
</syntaxhighlight> | |||
이 트리에서: | |||
* '''루트 노드''' - A | |||
* '''깊이''' - D, E, F의 깊이는 2 | |||
* '''차수''' - A의 차수는 2, B의 차수는 2, C의 차수는 1 | |||
* '''높이''' - 2 (루트 A에서 가장 깊은 리프까지의 거리 | |||
'''주의 사항은 "거리"는 간선의 수를 기준으로 한다는 것이다. 노드를 기준으로 3개 층이 있는 트리의 높이, 깊이는 모두 3이 아니라 2다.''' | |||
== 트리의 공식 == | |||
=== 높이와 노드 개수 관계 === | |||
이진 트리에서 '''높이 h'''와 '''최대 노드 수 N'''의 관계: | |||
* 최대 노드 개수: | |||
** N = 2<sup>(h+1)</sup> - 1 | |||
* 최소 노드 개수(편향 트리의 경우): | |||
** N = h + 1 | |||
=== 리프 노드 개수 공식 === | |||
* '''이진 트리에서 리프 노드 개수 L과 내부 노드 개수 N의 관계''' | |||
** L = N + 1 | |||
=== 균형 이진 트리에서 높이와 노드 개수 관계 === | |||
균형 잡힌 이진 트리(Balanced Binary Tree)에서: | |||
* 높이 h일 때 최소 노드 개수 | |||
** N = 2<sup>h</sup> - 1 | |||
* 높이 h일 때 최대 노드 개수 | |||
** N = 2<sup>(h+1)</sup> - 1 | |||
== 트리의 종류 == | |||
* '''일반 트리(General Tree)''': 노드가 제한 없이 여러 자식을 가질 수 있는 트리. | |||
* '''이진 트리(Binary Tree)''': 각 노드가 최대 두 개의 자식을 가질 수 있는 트리. | |||
* '''이진 탐색 트리(Binary Search Tree, BST)''': 왼쪽 자식은 부모보다 작은 값을, 오른쪽 자식은 부모보다 큰 값을 가지는 트리. | |||
* '''균형 이진 트리(Balanced Binary Tree)''': 높이를 균등하게 유지하는 트리 (예: AVL 트리, 레드-블랙 트리). | |||
* '''힙(Heap)''': 부모 노드가 자식 노드보다 크거나 작은 값을 가지는 트리. | |||
* '''B-트리(B-Tree)''': 데이터베이스 및 파일 시스템에서 사용되는 균형 트리. | |||
==트리의 활용== | |||
* '''검색 및 정렬''': | |||
** 검색: log(n)의 효율 | |||
** 정렬: [[힙|Heap]] 구조 이용 | |||
* '''파일 시스템''': 디렉터리 구조 표현. | |||
* '''데이터베이스''': B-트리 기반 인덱싱. | |||
** 인덱스: [[B 트리]], [[AVL 트리]], [[T 트리]] 등 | |||
* '''인공지능''': 의사 결정 트리(Decision Tree). | |||
* '''그래픽스''': 씬 그래프(Scene Graph) 구조. | |||
== 트리의 순회 == | ==트리의 순회== | ||
;Tree Traversal | ;Tree Traversal | ||
트리를 조회하는 방식 | 트리를 조회하는 방식 | ||
== [[이진 트리]] == | ======전위 순회(Preorder)====== | ||
*깊이 우선 순회(DFT, Depth-First Traversal) 라고도 하며, 주로 트리를 복사하거나 전위표기법을 구하는데 사용한다. | |||
*복사할 때 사용하는 이유는 트리의 노드부터 복사해야하기 때문이다. | |||
* 다음과 같은 방법으로 진행한다. | |||
*#노드를 방문한다. | |||
*#왼쪽 서브 트리를 전위 순회한다. | |||
*# 오른쪽 서브 트리를 전위 순회한다. | |||
======중위 순회(Inorder)====== | |||
* 대칭 순회(symmetric) 라고도 하며, 이진 탐색 트리(BST, Binary Search Tree) 에서 값을 가져올 때 주로 사용한다. | |||
*다음과 같은 방법으로 진행한다. | |||
*#왼쪽 서브 트리를 중위 순회한다. | |||
*#노드를 방문한다. | |||
*#오른쪽 서브 트리를 중위 순회한다. | |||
======후위 순회(Postorder)====== | |||
*값을 삭제할 때 주로 사용한다. 그 이유는 루트 노드를 지우기 전에 하위 노드를 먼저 지워야하기 때문이다. | |||
*다음과 같은 방법으로 진행한다. | |||
*#왼쪽 서브 트리를 후위 순회한다. | |||
*#오른쪽 서브 트리를 후위 순회한다. | |||
*#노드를 방문한다. | |||
======레벨 순서 순회(level-order)====== | |||
*너비 우선 순회(breadth-first traversal) 라고도 한다. | |||
*모든 노드를 낮은 레벨부터 차례대로 순회한다. | |||
==[[이진 트리]]== | |||
;Binary Tree | ;Binary Tree | ||
2025년 3월 7일 (금) 02:54 기준 최신판
Tree 트리(Tree)는 계층적 구조를 가지는 비선형 자료 구조로, 하나의 루트 노드(Root Node)에서 시작하여 여러 개의 자식 노드를 가질 수 있다. 트리는 그래프의 한 종류이며, 방향성이 있는 비순환 그래프(DAG, Directed Acyclic Graph)로 볼 수 있다.
트리의 특성[편집 | 원본 편집]
- 트리는 노드와 간선으로 구성된다.
- 순환(Cycle)이 존재하지 않는다.
- n개의 노드를 가진 트리는 항상 (n-1)개의 간선을 가진다.
- 루트에서 특정 노드까지의 경로는 유일하다.
관련 용어[편집 | 원본 편집]
| 용어 | 의미 |
|---|---|
| 차수(degree) | 노드의 부족 트리의 개수
|
| 단말 노드(leaf, terminal) | 차수가 0인, 가장 끝의 노드 |
| 내부 노드(internal) | 차수가 1 이상인, 단말이 아닌 노드 |
| 부모(parent) | 바로 상위 노드 |
| 자식(child) | 바로 하위 노드 |
| 형제(sibling) | 부모가 같은 노드 |
| 조상(ancestor) | 상위 노드, 부모 노드들의 집합 |
| 자손(descendant) | 하위 노드, 자식 노드들의 집합 |
| 레벨(level) | 상위 노드를 기준으로 한 깊이 |
| 깊이(depth) | 트리에 속한 최대 레벨 |
예시
A → 루트 노드 (깊이 0)
/ \
B C → 깊이 1
/ \ \
D E F → 깊이 2 (리프 노드: D, E, F)이 트리에서:
- 루트 노드 - A
- 깊이 - D, E, F의 깊이는 2
- 차수 - A의 차수는 2, B의 차수는 2, C의 차수는 1
- 높이 - 2 (루트 A에서 가장 깊은 리프까지의 거리
주의 사항은 "거리"는 간선의 수를 기준으로 한다는 것이다. 노드를 기준으로 3개 층이 있는 트리의 높이, 깊이는 모두 3이 아니라 2다.
트리의 공식[편집 | 원본 편집]
높이와 노드 개수 관계[편집 | 원본 편집]
이진 트리에서 높이 h와 최대 노드 수 N의 관계:
- 최대 노드 개수:
- N = 2(h+1) - 1
- 최소 노드 개수(편향 트리의 경우):
- N = h + 1
리프 노드 개수 공식[편집 | 원본 편집]
- 이진 트리에서 리프 노드 개수 L과 내부 노드 개수 N의 관계
- L = N + 1
균형 이진 트리에서 높이와 노드 개수 관계[편집 | 원본 편집]
균형 잡힌 이진 트리(Balanced Binary Tree)에서:
- 높이 h일 때 최소 노드 개수
- N = 2h - 1
- 높이 h일 때 최대 노드 개수
- N = 2(h+1) - 1
트리의 종류[편집 | 원본 편집]
- 일반 트리(General Tree): 노드가 제한 없이 여러 자식을 가질 수 있는 트리.
- 이진 트리(Binary Tree): 각 노드가 최대 두 개의 자식을 가질 수 있는 트리.
- 이진 탐색 트리(Binary Search Tree, BST): 왼쪽 자식은 부모보다 작은 값을, 오른쪽 자식은 부모보다 큰 값을 가지는 트리.
- 균형 이진 트리(Balanced Binary Tree): 높이를 균등하게 유지하는 트리 (예: AVL 트리, 레드-블랙 트리).
- 힙(Heap): 부모 노드가 자식 노드보다 크거나 작은 값을 가지는 트리.
- B-트리(B-Tree): 데이터베이스 및 파일 시스템에서 사용되는 균형 트리.
트리의 활용[편집 | 원본 편집]
- 검색 및 정렬:
- 검색: log(n)의 효율
- 정렬: Heap 구조 이용
- 파일 시스템: 디렉터리 구조 표현.
- 데이터베이스: B-트리 기반 인덱싱.
- 인공지능: 의사 결정 트리(Decision Tree).
- 그래픽스: 씬 그래프(Scene Graph) 구조.
트리의 순회[편집 | 원본 편집]
- Tree Traversal
트리를 조회하는 방식
전위 순회(Preorder)[편집 | 원본 편집]
- 깊이 우선 순회(DFT, Depth-First Traversal) 라고도 하며, 주로 트리를 복사하거나 전위표기법을 구하는데 사용한다.
- 복사할 때 사용하는 이유는 트리의 노드부터 복사해야하기 때문이다.
- 다음과 같은 방법으로 진행한다.
- 노드를 방문한다.
- 왼쪽 서브 트리를 전위 순회한다.
- 오른쪽 서브 트리를 전위 순회한다.
중위 순회(Inorder)[편집 | 원본 편집]
- 대칭 순회(symmetric) 라고도 하며, 이진 탐색 트리(BST, Binary Search Tree) 에서 값을 가져올 때 주로 사용한다.
- 다음과 같은 방법으로 진행한다.
- 왼쪽 서브 트리를 중위 순회한다.
- 노드를 방문한다.
- 오른쪽 서브 트리를 중위 순회한다.
후위 순회(Postorder)[편집 | 원본 편집]
- 값을 삭제할 때 주로 사용한다. 그 이유는 루트 노드를 지우기 전에 하위 노드를 먼저 지워야하기 때문이다.
- 다음과 같은 방법으로 진행한다.
- 왼쪽 서브 트리를 후위 순회한다.
- 오른쪽 서브 트리를 후위 순회한다.
- 노드를 방문한다.
레벨 순서 순회(level-order)[편집 | 원본 편집]
- 너비 우선 순회(breadth-first traversal) 라고도 한다.
- 모든 노드를 낮은 레벨부터 차례대로 순회한다.
이진 트리[편집 | 원본 편집]
- Binary Tree