K-최근접 이웃: 두 판 사이의 차이
IT 위키
편집 요약 없음 |
편집 요약 없음 |
||
| 1번째 줄: | 1번째 줄: | ||
[[분류:인공지능]][[분류:데이터 과학]] | [[분류:인공지능]][[분류:데이터 과학]] | ||
;K-nearest neighbor; KNN | ;K-nearest neighbor; KNN | ||
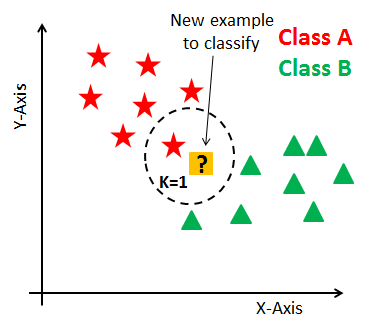
;k-최근접 이웃(k-Nearest Neighbors, kNN) 알고리즘은 '''모든 학습 데이터를 저장'''한 뒤, 새로운 데이터가 들어왔을 때 '''유사도 측정'''(similarity measure) 또는 | ;k-최근접 이웃(k-Nearest Neighbors, kNN) 알고리즘은 '''모든 학습 데이터를 저장'''한 뒤, 새로운 데이터가 들어왔을 때 '''유사도 측정'''(similarity '''measure) 또는 유사도 함수(similarity function)에 기반해 가장 가까운 데이터를 찾는 방식으로 예측을 수행하는 알고리즘이다. 이때 유사도는 일반적으로 유클리드 거리(Euclidean Distance)와 같은 거리를 사용해 계산된다.''' | ||
[[파일:Knn 예시.png]] | [[파일:Knn 예시.png]] | ||
| 20번째 줄: | 20번째 줄: | ||
#* '''분류''': 가장 가까운 k개의 이웃 데이터 포인트들 중 다수결을 통해 가장 많이 속하는 클래스로 분류한다. | #* '''분류''': 가장 가까운 k개의 이웃 데이터 포인트들 중 다수결을 통해 가장 많이 속하는 클래스로 분류한다. | ||
#* '''회귀''': k개의 이웃 데이터 포인트들의 평균을 사용하여 값을 예측한다. | #* '''회귀''': k개의 이웃 데이터 포인트들의 평균을 사용하여 값을 예측한다. | ||
'''예시''' | |||
예를 들어, 특정 사용자의 관심사를 예측하는 상황을 생각해보자. 이전에 수집된 사용자 데이터가 있으며, 각각의 사용자는 특정 장르의 영화를 선호하는 정보가 담겨 있다고 가정한다. | 예를 들어, 특정 사용자의 관심사를 예측하는 상황을 생각해보자. 이전에 수집된 사용자 데이터가 있으며, 각각의 사용자는 특정 장르의 영화를 선호하는 정보가 담겨 있다고 가정한다. | ||
| 29번째 줄: | 29번째 줄: | ||
# '''이웃 선택''': 가까운 k명의 사용자를 선택한다. | # '''이웃 선택''': 가까운 k명의 사용자를 선택한다. | ||
# '''투표''': k명의 사용자 중 가장 많이 선호하는 영화 장르를 선택하여 새로운 사용자가 선호할 가능성이 큰 장르를 예측한다. | # '''투표''': k명의 사용자 중 가장 많이 선호하는 영화 장르를 선택하여 새로운 사용자가 선호할 가능성이 큰 장르를 예측한다. | ||
== 활용 방법 및 팁 == | |||
* 사용할 데이터 속성, 거리 계산법, K값 등은 데이터와 예측 목표에 맞게 설정해야 한다. | |||
* [[의사결정 나무]]의 가지치기와 같은 과정이 없으므로 불필요한 속성이 너무 많으면 전혀 예측이 되지 않는다. | |||
* | |||
== 장단점 == | == 장단점 == | ||
2024년 10월 29일 (화) 08:41 판
- K-nearest neighbor; KNN
- k-최근접 이웃(k-Nearest Neighbors, kNN) 알고리즘은 모든 학습 데이터를 저장한 뒤, 새로운 데이터가 들어왔을 때 유사도 측정(similarity measure) 또는 유사도 함수(similarity function)에 기반해 가장 가까운 데이터를 찾는 방식으로 예측을 수행하는 알고리즘이다. 이때 유사도는 일반적으로 유클리드 거리(Euclidean Distance)와 같은 거리를 사용해 계산된다.
주요 특징
- 비모수적(non-parametric): kNN은 데이터에 대해 특정 함수 형태를 가정하지 않는다. 이는 여러 유형의 데이터에 대해 유연하게 적용할 수 있어 강력한 이점을 제공하지만, 반대로 데이터에 지나치게 적합되는 과적합(overfitting) 문제를 일으킬 수 있다.
- 훈련 과정이 없음: kNN은 사전 학습(training) 단계가 없다. 즉, 모델이 학습되지 않으며, 예측할 때 직접 계산을 수행한다. 이러한 특성 때문에 게으른 학습(lazy learning) 또는 인스턴스 기반 학습(instance-based learning) 알고리즘으로도 불린다.
- 예측 시 느림: 훈련된 모델을 미리 저장하지 않기 때문에 예측 단계에서 모든 데이터를 참고해야 하며, 특히 데이터셋이 클수록 많은 시간이 소요된다. 이는 예측이 빠른 다른 알고리즘에 비해 단점으로 작용할 수 있다.
- 널리 사용됨: 직관적이고 이해하기 쉬운 알고리즘으로, 다양한 분류와 회귀 문제에 활용된다.
작동 방식
- 데이터 준비: 각 데이터 포인트의 위치와 해당하는 클래스(또는 값)를 포함한 학습 데이터를 준비한다.
- 거리 계산: 새로운 데이터 포인트가 주어지면, 학습 데이터와의 거리를 계산한다.
- 가장 가까운 k개의 이웃 선택: 계산된 거리 중 가장 가까운 k개의 데이터 포인트를 선택한다.
- 투표:
- 분류: 가장 가까운 k개의 이웃 데이터 포인트들 중 다수결을 통해 가장 많이 속하는 클래스로 분류한다.
- 회귀: k개의 이웃 데이터 포인트들의 평균을 사용하여 값을 예측한다.
예시
예를 들어, 특정 사용자의 관심사를 예측하는 상황을 생각해보자. 이전에 수집된 사용자 데이터가 있으며, 각각의 사용자는 특정 장르의 영화를 선호하는 정보가 담겨 있다고 가정한다.
- 데이터 준비: 각 사용자의 나이와 영화 장르 선호도가 포함된 데이터를 준비한다.
- 새로운 사용자 정보 입력: 예를 들어, 나이가 30살인 새로운 사용자가 입력된다.
- 거리 계산: 이 새로운 사용자가 기존 사용자와 얼마나 가까운지(예: 나이 차이를 기준으로) 계산한다.
- 이웃 선택: 가까운 k명의 사용자를 선택한다.
- 투표: k명의 사용자 중 가장 많이 선호하는 영화 장르를 선택하여 새로운 사용자가 선호할 가능성이 큰 장르를 예측한다.
활용 방법 및 팁
- 사용할 데이터 속성, 거리 계산법, K값 등은 데이터와 예측 목표에 맞게 설정해야 한다.
- 의사결정 나무의 가지치기와 같은 과정이 없으므로 불필요한 속성이 너무 많으면 전혀 예측이 되지 않는다.
장단점
k-최근접 이웃(k-Nearest Neighbors, kNN) 알고리즘은 직관적이고 구현이 쉬운 장점이 있지만, 몇 가지 단점과 제약 사항도 함께 가지고 있다. 아래는 kNN의 주요 장점과 단점을 요약한 내용이다.
kNN의 단점
- 많은 저장 공간 필요: kNN은 모든 학습 데이터를 저장해야 하기 때문에 큰 데이터셋을 다룰 경우 상당한 저장 공간이 필요하다.
- 예측 시간 지연: 새로운 데이터를 분류할 때, 모든 데이터를 참고해야 하므로 시간이 많이 걸릴 수 있다. 이는 사전에 훈련된 모델로 빠르게 예측을 수행할 수 있는 알고리즘에 비해 불리하다.
- 거리 함수 설계의 중요성: 적절한 거리 함수나 유사도 함수를 설정해야 하고, 이를 위해 도메인 지식이 필요할 수 있다. 거리 측정 방식이 데이터의 실제 관계를 잘 반영하지 못하면, 예측 성능이 크게 저하될 수 있다.
- 최상의 모델이 아님: kNN은 보통 성능 면에서 다른 고성능 알고리즘보다 뒤처질 수 있다. 따라서 항상 최고의 예측 성능을 제공하지는 않는다.
- 변수 크기 조정 문제: 입력 변수의 크기가 서로 다르면 거리 계산에 큰 영향을 줄 수 있다. 이를 해결하기 위해 정규화(normalization) 또는 표준화(standardization) 작업이 필요하다.
kNN의 장점
- 간단한 구현과 사용: 알고리즘이 직관적이고 코드 구현이 쉬워서 초보자도 사용하기 용이하다.
- 다양한 클래스 지원: 결과값으로 여러 개의 클래스를 가질 수 있어, 이진 분류뿐만 아니라 다중 클래스 분류도 가능하다.
- 유연한 점수 계산 방식: 클래스 간 비율이나 가중치를 임의로 조정할 수 있어 다양한 예측 방법을 시도할 수 있다.
- 설명 가능한 예측 방식: 가까운 이웃에 기반해 예측하기 때문에, 결과를 이해하고 설명하기가 쉽다. 이는 예측의 투명성과 해석력을 높인다.
- 도메인 지식 반영 가능: 거리 함수를 도메인 지식에 맞게 조정할 수 있어, 특정 분야의 데이터에 맞게 커스터마이징이 가능하다.
- 쉽게 업데이트 가능: 새로운 데이터가 추가되면 기존 데이터를 변경하지 않고 추가할 수 있어 실시간 학습이나 지속적인 데이터 업데이트에 유리하다.
- 범용 함수로 사용 가능: 다양한 함수 형태를 취할 수 있어, 특정 문제에 맞게 유연하게 설정하여 사용할 수 있다.