트리
From IT Wiki
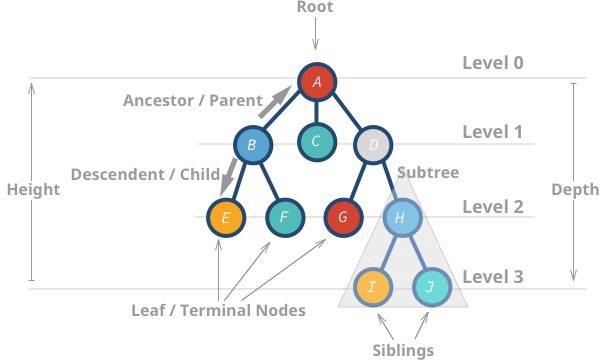
관련 용어[edit | edit source]
| 용어 | 의미 |
|---|---|
| 차수(degree) | 노드의 부족 트리의 개수
|
| 단말 노드(leaf, terminal) | 차수가 0인, 가장 끝의 노드 |
| 내부 노드(internal) | 차수가 1 이상인, 단말이 아닌 노드 |
| 부모(parent) | 바로 상위 노드 |
| 자식(child) | 바로 하위 노드 |
| 형제(sibling) | 부모가 같은 노드 |
| 조상(ancestor) | 상위 노드, 부모 노드들의 집합 |
| 자손(descendant) | 하위 노드, 자식 노드들의 집합 |
| 레벨(level) | 상위 노드를 기준으로 한 깊이 |
| 깊이(depth) | 트리에 속한 최대 레벨 |
트리의 활용[edit | edit source]
트리의 순회[edit | edit source]
- Tree Traversal
트리를 조회하는 방식
전위 순회(Preorder)[edit | edit source]
- 깊이 우선 순회(DFT, Depth-First Traversal) 라고도 하며, 주로 트리를 복사하거나 전위표기법을 구하는데 사용한다.[1]
- 복사할 때 사용하는 이유는 트리의 노드부터 복사해야하기 때문이다.
- 다음과 같은 방법으로 진행한다.
- 노드를 방문한다.
- 왼쪽 서브 트리를 전위 순회한다.
- 오른쪽 서브 트리를 전위 순회한다.
중위 순회(Inorder)[edit | edit source]
- 대칭 순회(symmetric) 라고도 하며, 이진 탐색 트리(BST, Binary Search Tree) 에서 값을 가져올 때 주로 사용한다.
- 다음과 같은 방법으로 진행한다.
- 왼쪽 서브 트리를 중위 순회한다.
- 노드를 방문한다.
- 오른쪽 서브 트리를 중위 순회한다.
후위 순회(Postorder)[edit | edit source]
- 값을 삭제할 때 주로 사용한다. 그 이유는 루트 노드를 지우기 전에 하위 노드를 먼저 지워야하기 때문이다.
- 다음과 같은 방법으로 진행한다.
- 왼쪽 서브 트리를 후위 순회한다.
- 오른쪽 서브 트리를 후위 순회한다.
- 노드를 방문한다.
레벨 순서 순회(level-order)[edit | edit source]
- 너비 우선 순회(breadth-first traversal) 라고도 한다.
- 모든 노드를 낮은 레벨부터 차례대로 순회한다.
이진 트리[edit | edit source]
- Binary Tree