삼각 분할
삼각 분할(Triangulation)은 다각형을 삼각형들의 집합으로 나누는 과정으로, 계산 기하학, 컴퓨터 그래픽스, 지형 모델링 등 다양한 분야에서 활용된다.
1 개요
삼각 분할은 다각형을 겹치지 않는 삼각형으로 분할하는 방법으로, 각 변(chord)이 기존의 다각형의 변이거나 다른 변과 교차하지 않는 방식으로 구성된다. 일반적으로 단순 다각형에 대해 삼각 분할을 수행하며, 특정 알고리즘을 통해 자동으로 삼각형 집합을 생성할 수 있다.
간단한 예제
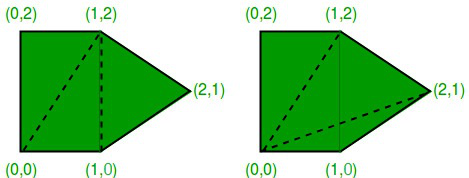
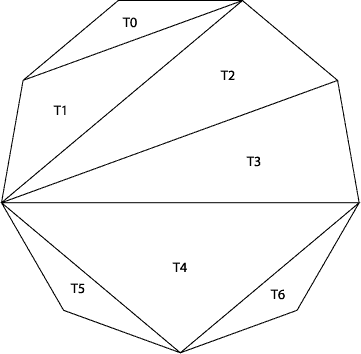
이렇게 하나의 도형을 어떤식으로 삼각형으로 나눌 지는 도형이 각을 많이 가질 수록 다양해질 수 있다. 기본적으로 일반적인 형태의 N각형의 경우 아래의 공식이 성립한다.
기본 N각형일 때의 규칙
- 나누어지는 삼각형은 N-2가 된다.
- 사용되는 선은 N-3이 된다.
2 구분
삼각 분할 알고리즘은 용도에 따라 다양한 이름으로 불리고 다양한 접근법이 존재한다. 먼저 기본적인 N각형(Regular Polygon)을 다루는 경우와 복잡한 형태의 도형을 다루는 경우가 있다. 여기서 Regular Polygon은 본질적으로는 Convex Polygon(볼록 다각형)과 동일하다. 위에서 나온 ⌂ 모양의 5각형도 일반적인 정오각형은 아니지만 오각형과 접근법은 거의 동일하다. (일부 최적화 기준에 따라 달라질 수는 있음)
이런 볼록 다각형의 경우엔 상대적으로 쉬우면서도, 현실적으로 가능하기 때문에 최적화 문제로 많이 접근이 된다. Optimal Triangulation 문제는 동적 계획법을 배우기 위한 알고리즘 문제로 유명하다.
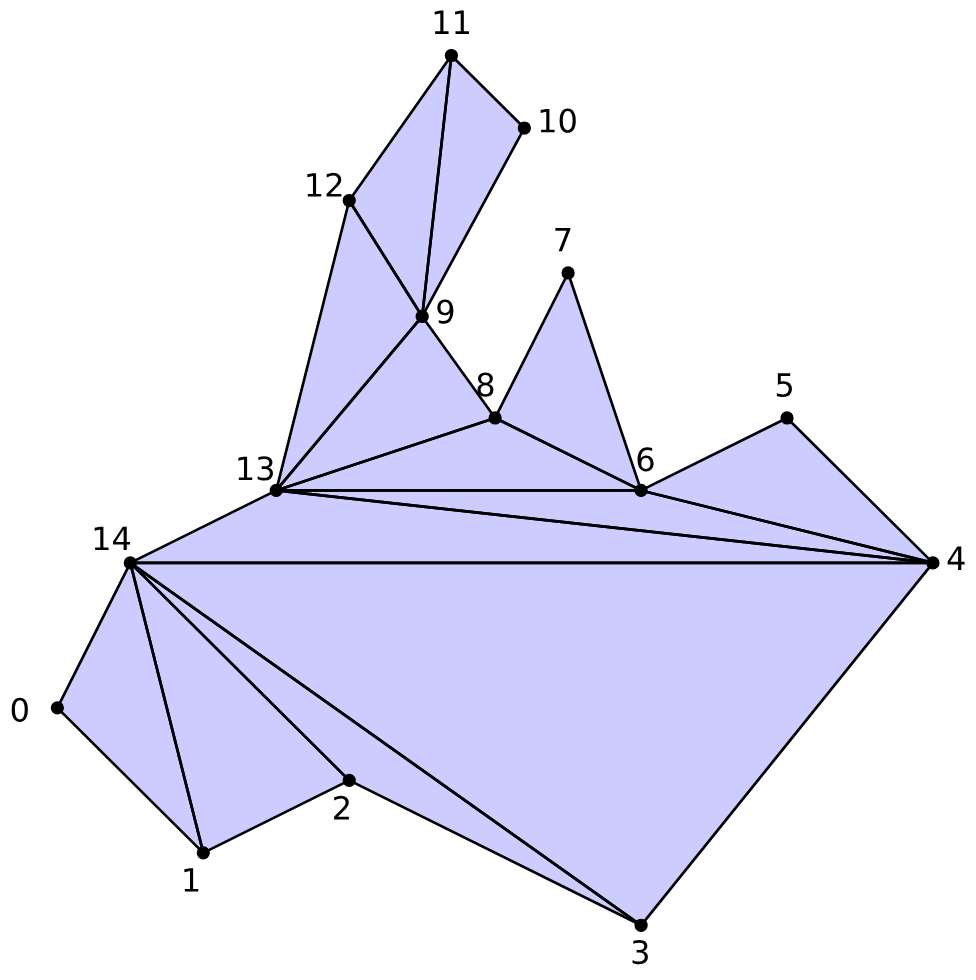
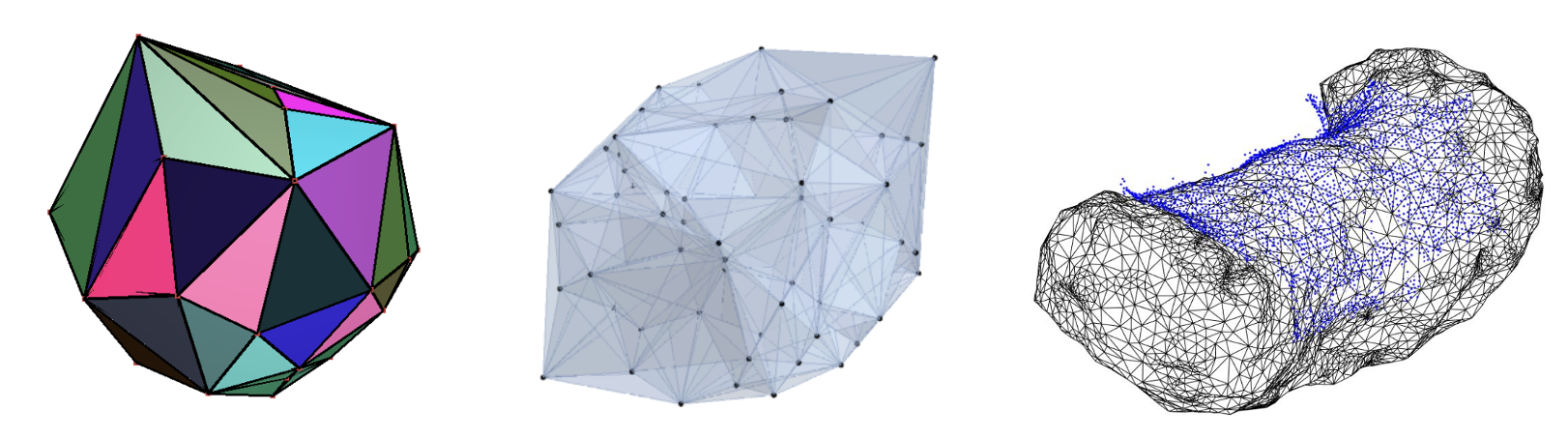
다만 볼록 다각형이 아닌 경우에는 용도와 접근법이 완전히 다르다. 3D 그래필을 표현할 때 표현을 나누는 용도로 사용되기도 하고, 실제 지형 분석에서 지형을 구분하는 접근법으로 실용적으로 쓰이기도 한다.
3 알고리즘
삼각 분할을 수행하는 대표적인 알고리즘은 다음과 같다.
- 귀퉁이 잘라내기(Ear Clipping) 알고리즘
- 단순 다각형의 내부 삼각형을 하나씩 제거하는 방식
- O(n²) 시간 복잡도를 가짐
- 분할 정복 알고리즘
- 다각형을 작은 부분으로 나눈 후 병합하여 삼각 분할 수행
- O(n log n) 시간 복잡도를 가짐
- 모노톤 다각형 분할
- 다각형을 단조 다각형으로 나눈 후 삼각화하는 방식
- O(n log n)에서 최적화하면 O(n) 시간 복잡도를 가짐
4 예제 코드
다음은 Python을 사용하여 귀퉁이 잘라내기(Ear Clipping) 알고리즘을 이용한 삼각 분할 예제이다.
import numpy as np
def is_convex(p1, p2, p3):
""" 세 점이 시계 방향인지 확인 """
return (p2[0] - p1[0]) * (p3[1] - p2[1]) - (p2[1] - p1[1]) * (p3[0] - p2[0]) < 0
def ear_clipping_triangulation(polygon):
""" Ear Clipping을 이용한 삼각 분할 """
points = polygon.copy()
triangles = []
while len(points) > 3:
for i in range(len(points)):
prev, curr, next = points[i-1], points[i], points[(i+1) % len(points)]
if is_convex(prev, curr, next):
triangles.append([prev, curr, next])
del points[i] # 귀(Ear) 제거
break
triangles.append(points) # 마지막 삼각형 추가
return triangles
# 예제 다각형 (오각형)
polygon = np.array([
[0, 0], [2, 0], [3, 1], [1, 2], [0, 1]
])
triangles = ear_clipping_triangulation(polygon)
for t in triangles:
print(t)
5 활용
- 컴퓨터 그래픽스 - 3D 모델링에서 메시(mesh) 생성에 사용
- 지형 모델링 - 지리정보시스템(GIS)에서 지형을 삼각형 기반으로 표현
- 물리 시뮬레이션 - 유한 요소법(FEM)에서 복잡한 도형을 삼각형 요소로 변환
- 로봇 경로 계획 - 환경을 삼각형으로 나누어 탐색 및 이동 경로 최적화
6 같이 보기
7 참고 문헌
- de Berg, M., Cheong, O., van Kreveld, M., & Overmars, M. (2008). Computational Geometry: Algorithms and Applications. Springer.
- Preparata, F. P., & Shamos, M. I. (1985). Computational Geometry: An Introduction. Springer.