스크램블링 인코딩: 두 판 사이의 차이
IT 위키
(새 문서: '''Scrambling Technique''' 스크램블링 기법은 독자적인 인코딩 기법이라 보긴 어렵고 다른 인코딩 방식에서 발생할 수 있는 문제점을 보완하는 기법이라고 보아야 한다. == 스크램블링 기법 == Scrambling은 특정 비트열이 신호 상에서 일정한 전압 상태(예: 지속적인 0 또는 +, -의 패턴)를 발생시키는 문제를 해결하기 위한 기술이다. 주요 목적은 데이터를 전송할 때 신호의...) |
편집 요약 없음 |
||
| 24번째 줄: | 24번째 줄: | ||
* '''[[이중 위상 인코딩|Bipolar-AMI]]''' 기반의 Scrambling 기법. | * '''[[이중 위상 인코딩|Bipolar-AMI]]''' 기반의 Scrambling 기법. | ||
* '''목적''': 연속된 8개의 0을 포함하는 비트 패턴을 변환하여 AMI 코드에서 발생하는 문제를 해결함 | * '''목적''': 연속된 8개의 0을 포함하는 비트 패턴을 변환하여 AMI 코드에서 발생하는 문제를 해결함 | ||
* '''방법''': | * '''방법''': | ||
** '''8개의 0이 연속으로 나타날 때''', 그 직전 신호가 양(+)이었으면 | ** '''8개의 0이 연속으로 나타날 때''', 그 직전 신호가 양(+)이었으면 '''0 0 0 + - 0 - +''' 로 인코딩 | ||
** '''8개의 0이 연속으로 나타날 때''', 그 직전 신호가 음(-)이었으면 | ** '''8개의 0이 연속으로 나타날 때''', 그 직전 신호가 음(-)이었으면 '''0 0 0 - + 0 + -''' 로 인코딩 | ||
** 이 방식은 AMI 코드의 두 가지 위반을 유발하는데, 이는 '''잡음에 의해 자연적으로 발생할 가능성이 매우 낮음''' | ** 이 방식은 AMI 코드의 두 가지 위반을 유발하는데, 이는 '''잡음에 의해 자연적으로 발생할 가능성이 매우 낮음''' | ||
** 수신기는 이 패턴을 감지하고 이를 원래의 '''8개의 0''' 비트열로 해석함. | ** 수신기는 이 패턴을 감지하고 이를 원래의 '''8개의 0''' 비트열로 해석함 | ||
=== 알고리즘 코드 (파이썬) === | |||
<syntaxhighlight lang="python3" line="1"> | |||
def b8zs(nrzl_input): | |||
output = [] | |||
previous_pulse = 1 # Assume initial pulse is positive | |||
zero_count = 0 | |||
for bit in nrzl_input: | |||
if bit == 1: | |||
# Alternate the pulse for '1' | |||
pulse = previous_pulse | |||
output.append(pulse) | |||
previous_pulse = -previous_pulse | |||
zero_count = 0 # Reset zero counter | |||
else: | |||
zero_count += 1 | |||
if zero_count == 8: | |||
# 8 consecutive zeros detected, apply B8ZS substitution | |||
if previous_pulse == 1: | |||
# Last pulse was positive | |||
output.extend([0, 0, 0, 1, -1, 0, -1, 1]) # 000+-0-+ | |||
else: | |||
# Last pulse was negative | |||
output.extend([0, 0, 0, -1, 1, 0, 1, -1]) # 000-+0+- | |||
zero_count = 0 | |||
else: | |||
output.append(0) # Regular zero | |||
return output | |||
# 테스트 데이터 (NRZ-L 입력값) | |||
nrzl_input_1 = [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0] | |||
nrzl_input_2 = [1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1] | |||
# B8ZS 테스트 | |||
print("B8ZS encoding:", b8zs(nrzl_input_1)) | |||
print("B8ZS encoding:", b8zs(nrzl_input_2)) | |||
</syntaxhighlight>실행 결과 | |||
* B8ZS encoding: [1, 0, 0, 0, 0, 0, 0, 1, -1, 0, -1, 1, -1, 0, 1, 0, -1] | |||
* B8ZS encoding: [1, 0, -1, 0, 0, 0, 0, 1, -1, 0, -1, 1, 1, -1, 0, 1] | |||
== HDB3 == | == HDB3 == | ||
| 51번째 줄: | 93번째 줄: | ||
| -00- | | -00- | ||
|} | |} | ||
=== 알고리즘 코드 (파이썬) === | |||
<syntaxhighlight lang="python3" line="1"> | |||
def hdb3(nrzl_input): | |||
output = [] | |||
previous_pulse = 1 # Assume the initial pulse is positive | |||
one_count = 0 # Number of ones since the last substitution | |||
zero_count = 0 | |||
for bit in nrzl_input: | |||
if bit == 1: | |||
# Handling a 1 bit | |||
if previous_pulse == 1: | |||
output.append(1) # Positive pulse | |||
else: | |||
output.append(-1) # Negative pulse | |||
previous_pulse = -previous_pulse # Toggle the pulse | |||
one_count += 1 | |||
zero_count = 0 # Reset zero count after a 1 | |||
else: | |||
zero_count += 1 | |||
if zero_count == 4: | |||
# Four consecutive zeros detected -> HDB3 substitution | |||
if one_count % 2 == 0: | |||
# Even number of ones: B00B pattern | |||
if previous_pulse == 1: | |||
output.extend([-1, 0, 0, -1]) # -00- | |||
else: | |||
output.extend([1, 0, 0, 1]) # +00+ | |||
else: | |||
# Odd number of ones: 000V pattern | |||
if previous_pulse == 1: | |||
output.extend([0, 0, 0, 1]) # 000+ | |||
else: | |||
output.extend([0, 0, 0, -1]) # 000- | |||
zero_count = 0 | |||
one_count = 0 # Reset one count after substitution | |||
else: | |||
output.append(0) # Regular 0 handling | |||
return output | |||
# Test data (NRZ-L input) | |||
nrzl_input_1 = [1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1] | |||
nrzl_input_2 = [0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0] | |||
# HDB3 test | |||
print("HDB3 encoding:", hdb3(nrzl_input_1)) | |||
print("HDB3 encoding:", hdb3(nrzl_input_2)) | |||
</syntaxhighlight>실행 결과 | |||
* HDB3 encoding: [1, 0, 0, 0, 0, 0, 0, -1, -1, 0, 0, 0, 0, 0, 0, 1, 0, 1, -1, 0, 0, 1] | |||
* HDB3 encoding: [0, 0, 0, -1, 0, 0, -1, 1, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, -1, 1, -1, 0] | |||
2024년 10월 10일 (목) 03:38 판
Scrambling Technique
스크램블링 기법은 독자적인 인코딩 기법이라 보긴 어렵고 다른 인코딩 방식에서 발생할 수 있는 문제점을 보완하는 기법이라고 보아야 한다.
스크램블링 기법
Scrambling은 특정 비트열이 신호 상에서 일정한 전압 상태(예: 지속적인 0 또는 +, -의 패턴)를 발생시키는 문제를 해결하기 위한 기술이다. 주요 목적은 데이터를 전송할 때 신호의 동기화 문제를 해결하고, DC(직류) 성분을 없애는 것이다.
- 대체 신호 패턴(Filling Sequence)
- 연속된 0 또는 다른 일정한 패턴이 발생할 경우 이를 대체할 신호 패턴을 삽입
- 동기화를 유지하기 위해 충분한 신호 변화를 만들어야 함
- 수신기는 대체된 신호 패턴을 인식하고 이를 원래 데이터로 복구해야 함
- 대체된 신호의 길이는 원래 신호와 동일해야 함
- 디자인 목표
- DC 성분 없음
- 장기간의 동일 레벨의 신호 없음
- 데이터 전송률 저하 없음
- 에러 탐지 기능
예시
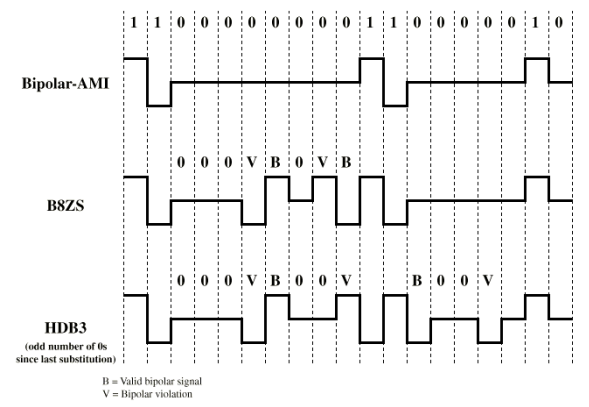
B8ZS
Bipolar with 8 Zeros Substitution
- Bipolar-AMI 기반의 Scrambling 기법.
- 목적: 연속된 8개의 0을 포함하는 비트 패턴을 변환하여 AMI 코드에서 발생하는 문제를 해결함
- 방법:
- 8개의 0이 연속으로 나타날 때, 그 직전 신호가 양(+)이었으면 0 0 0 + - 0 - + 로 인코딩
- 8개의 0이 연속으로 나타날 때, 그 직전 신호가 음(-)이었으면 0 0 0 - + 0 + - 로 인코딩
- 이 방식은 AMI 코드의 두 가지 위반을 유발하는데, 이는 잡음에 의해 자연적으로 발생할 가능성이 매우 낮음
- 수신기는 이 패턴을 감지하고 이를 원래의 8개의 0 비트열로 해석함
알고리즘 코드 (파이썬)
def b8zs(nrzl_input):
output = []
previous_pulse = 1 # Assume initial pulse is positive
zero_count = 0
for bit in nrzl_input:
if bit == 1:
# Alternate the pulse for '1'
pulse = previous_pulse
output.append(pulse)
previous_pulse = -previous_pulse
zero_count = 0 # Reset zero counter
else:
zero_count += 1
if zero_count == 8:
# 8 consecutive zeros detected, apply B8ZS substitution
if previous_pulse == 1:
# Last pulse was positive
output.extend([0, 0, 0, 1, -1, 0, -1, 1]) # 000+-0-+
else:
# Last pulse was negative
output.extend([0, 0, 0, -1, 1, 0, 1, -1]) # 000-+0+-
zero_count = 0
else:
output.append(0) # Regular zero
return output
# 테스트 데이터 (NRZ-L 입력값)
nrzl_input_1 = [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0]
nrzl_input_2 = [1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1]
# B8ZS 테스트
print("B8ZS encoding:", b8zs(nrzl_input_1))
print("B8ZS encoding:", b8zs(nrzl_input_2))
실행 결과
- B8ZS encoding: [1, 0, 0, 0, 0, 0, 0, 1, -1, 0, -1, 1, -1, 0, 1, 0, -1]
- B8ZS encoding: [1, 0, -1, 0, 0, 0, 0, 1, -1, 0, -1, 1, 1, -1, 0, 1]
HDB3
- Bipolar-AMI 기반의 또 다른 Scrambling 기법.
- 목적: 4개의 0가 연속되는 비트열을 처리하기 위해 설계됨.
- 방법: 연속된 4개의 0을 하나 또는 두 개의 펄스로 대체하여 AMI 코드 위반을 유발하지만, 그 패턴은 수신기가 쉽게 인식할 수 있음.
| 직전 펄스 | N이 홀수 | N이 짝수 |
|---|---|---|
| - | 000- | +00+ |
| + | 000+ | -00- |
알고리즘 코드 (파이썬)
def hdb3(nrzl_input):
output = []
previous_pulse = 1 # Assume the initial pulse is positive
one_count = 0 # Number of ones since the last substitution
zero_count = 0
for bit in nrzl_input:
if bit == 1:
# Handling a 1 bit
if previous_pulse == 1:
output.append(1) # Positive pulse
else:
output.append(-1) # Negative pulse
previous_pulse = -previous_pulse # Toggle the pulse
one_count += 1
zero_count = 0 # Reset zero count after a 1
else:
zero_count += 1
if zero_count == 4:
# Four consecutive zeros detected -> HDB3 substitution
if one_count % 2 == 0:
# Even number of ones: B00B pattern
if previous_pulse == 1:
output.extend([-1, 0, 0, -1]) # -00-
else:
output.extend([1, 0, 0, 1]) # +00+
else:
# Odd number of ones: 000V pattern
if previous_pulse == 1:
output.extend([0, 0, 0, 1]) # 000+
else:
output.extend([0, 0, 0, -1]) # 000-
zero_count = 0
one_count = 0 # Reset one count after substitution
else:
output.append(0) # Regular 0 handling
return output
# Test data (NRZ-L input)
nrzl_input_1 = [1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1]
nrzl_input_2 = [0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0]
# HDB3 test
print("HDB3 encoding:", hdb3(nrzl_input_1))
print("HDB3 encoding:", hdb3(nrzl_input_2))
실행 결과
- HDB3 encoding: [1, 0, 0, 0, 0, 0, 0, -1, -1, 0, 0, 0, 0, 0, 0, 1, 0, 1, -1, 0, 0, 1]
- HDB3 encoding: [0, 0, 0, -1, 0, 0, -1, 1, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, -1, 1, -1, 0]