멀티 레이어 퍼셉트론: 두 판 사이의 차이
(새 문서: 멀티 레이어 퍼셉트론(Multi‑Layer Perceptron, MLP)은 입력층, 하나 이상의 은닉층 및 출력층으로 구성된 완전 연결(feedforward) 인공 신경망이다. ==구조== MLP는 최소 세 개의 층, 즉 입력층, 하나 이상의 은닉층(hidden layer), 그리고 출력층(output layer)으로 구성된다. 각 은닉층과 출력층의 뉴런은 이전 층의 모든 뉴런과 완전하게 연결되어 있다. ==활성화 함수== MLP에서는 각 뉴...) |
편집 요약 없음 |
||
| 1번째 줄: | 1번째 줄: | ||
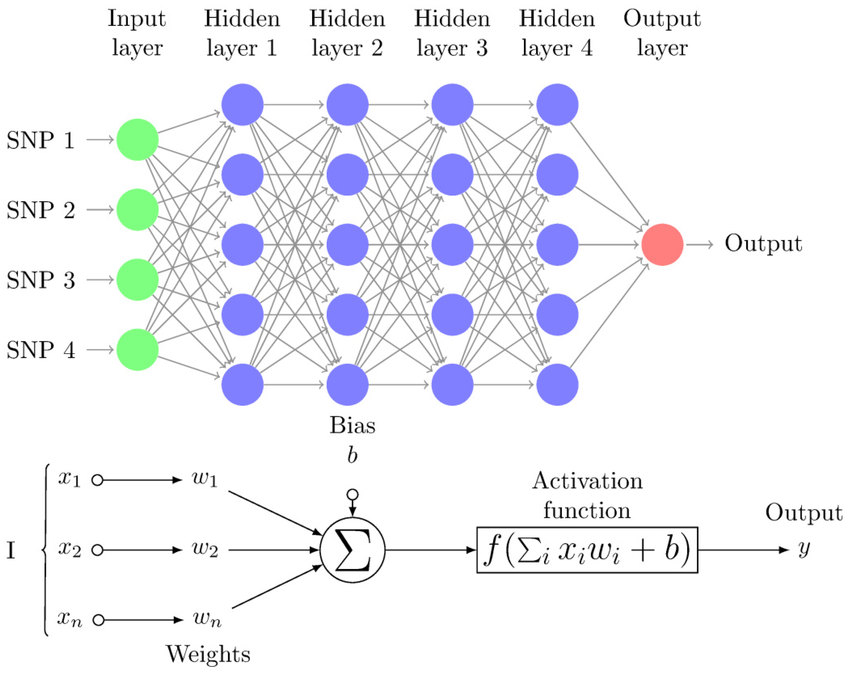
[[파일:멀티 레이어 퍼셉트론 구조.png|섬네일|멀티 레이어 퍼셉트론 구조]] | |||
멀티 레이어 퍼셉트론(Multi‑Layer Perceptron, MLP)은 입력층, 하나 이상의 은닉층 및 출력층으로 구성된 완전 연결(feedforward) 인공 신경망이다. | 멀티 레이어 퍼셉트론(Multi‑Layer Perceptron, MLP)은 입력층, 하나 이상의 은닉층 및 출력층으로 구성된 완전 연결(feedforward) 인공 신경망이다. | ||
==구조== | ==구조== | ||
| 7번째 줄: | 8번째 줄: | ||
MLP는 오차역전파(backpropagation) 알고리즘과 경사하강법(gradient descent)을 이용해 학습한다. 학습 과정에서 출력값과 목표값의 차이(error)를 계산하고 이를 기반으로 가중치(weight)를 조정한다. | MLP는 오차역전파(backpropagation) 알고리즘과 경사하강법(gradient descent)을 이용해 학습한다. 학습 과정에서 출력값과 목표값의 차이(error)를 계산하고 이를 기반으로 가중치(weight)를 조정한다. | ||
==장단점== | ==장단점== | ||
MLP는 비선형 함수 근사에 뛰어난 능력을 지니며, 분류(classification)나 회귀(regression) 문제에도 널리 사용된다. 그러나 은닉층 수, 뉴런 수 등 하이퍼파라미터에 민감하며, | MLP는 비선형 함수 근사에 뛰어난 능력을 지니며, 분류(classification)나 회귀(regression) 문제에도 널리 사용된다. 그러나 은닉층 수, 뉴런 수 등 하이퍼파라미터에 민감하며, 비볼록 손실 함수(non-convex loss)를 가지기 때문에 초기화 방식에 따라 결과가 달라질 수 있다. 또한 특성(feature) 스케일에 민감한 단점도 있다. | ||
==역할 및 응용== | ==역할 및 응용== | ||
MLP는 심층 신경망(deep neural network)의 가장 기본적인 형태로, 딥러닝(deep learning)의 근간이 되는 구조이다. 이미지 인식, 음성 인식, 텍스트 분류 등에서 널리 활용된다. | MLP는 심층 신경망(deep neural network)의 가장 기본적인 형태로, 딥러닝(deep learning)의 근간이 되는 구조이다. 이미지 인식, 음성 인식, 텍스트 분류 등에서 널리 활용된다. | ||
2025년 9월 11일 (목) 01:47 기준 최신판
멀티 레이어 퍼셉트론(Multi‑Layer Perceptron, MLP)은 입력층, 하나 이상의 은닉층 및 출력층으로 구성된 완전 연결(feedforward) 인공 신경망이다.
구조[편집 | 원본 편집]
MLP는 최소 세 개의 층, 즉 입력층, 하나 이상의 은닉층(hidden layer), 그리고 출력층(output layer)으로 구성된다. 각 은닉층과 출력층의 뉴런은 이전 층의 모든 뉴런과 완전하게 연결되어 있다.
활성화 함수[편집 | 원본 편집]
MLP에서는 각 뉴런의 출력에 sigmoid, tanh 또는 ReLU와 같은 비선형 활성화 함수(activation function)를 사용한다. 이러한 비선형성 덕분에 MLP는 선형적으로 분리되지 않는 데이터를 사용할 수 있게 된다.
학습 방법[편집 | 원본 편집]
MLP는 오차역전파(backpropagation) 알고리즘과 경사하강법(gradient descent)을 이용해 학습한다. 학습 과정에서 출력값과 목표값의 차이(error)를 계산하고 이를 기반으로 가중치(weight)를 조정한다.
장단점[편집 | 원본 편집]
MLP는 비선형 함수 근사에 뛰어난 능력을 지니며, 분류(classification)나 회귀(regression) 문제에도 널리 사용된다. 그러나 은닉층 수, 뉴런 수 등 하이퍼파라미터에 민감하며, 비볼록 손실 함수(non-convex loss)를 가지기 때문에 초기화 방식에 따라 결과가 달라질 수 있다. 또한 특성(feature) 스케일에 민감한 단점도 있다.
역할 및 응용[편집 | 원본 편집]
MLP는 심층 신경망(deep neural network)의 가장 기본적인 형태로, 딥러닝(deep learning)의 근간이 되는 구조이다. 이미지 인식, 음성 인식, 텍스트 분류 등에서 널리 활용된다.
같이 보기[편집 | 원본 편집]
참고 문헌[편집 | 원본 편집]
- Ian Goodfellow, Yoshua Bengio, Aaron Courville, 《Deep Learning》, MIT Press
- Simon Haykin, 《Neural Networks: A Comprehensive Foundation》, Prentice Hall