배치 정규화: 두 판 사이의 차이
IT 위키
(새 문서: 배치 정규화(영어: Batch Normalization, 줄여서 BN)는 딥 러닝에서 학습을 안정화하고 속도를 향상시키기 위해 사용되는 정규화 기법이다. 각 층의 입력을 정규화하여 내부 공변량 변화(Internal Covariate Shift)를 줄이는 것을 목적으로 한다. ==개요== *딥러닝 모델은 층이 깊어질수록 학습이 불안정해지고, 기울기 소실/폭주 문제로 인해 학습 속도가 느려진다. *배치 정규화는...) |
편집 요약 없음 |
||
| 4번째 줄: | 4번째 줄: | ||
*배치 정규화는 미니배치 단위로 입력의 평균과 분산을 계산해 정규화한 뒤, 학습 가능한 스케일(scale)과 이동(shift) 파라미터를 적용한다. | *배치 정규화는 미니배치 단위로 입력의 평균과 분산을 계산해 정규화한 뒤, 학습 가능한 스케일(scale)과 이동(shift) 파라미터를 적용한다. | ||
*이 과정을 통해 각 층의 입력 분포를 일정하게 유지하여 학습을 원활히 한다. | *이 과정을 통해 각 층의 입력 분포를 일정하게 유지하여 학습을 원활히 한다. | ||
예를 들면<blockquote>Dense 출력값: [-1.2, 0.3, 2.0, -0.8, ...] | |||
'''↓ BN (정규화)''' | |||
정규화 후: [-0.9, -0.1, 0.8, -0.5, ...] (평균 ≈ 0) | |||
'''↓ ReLU''' | |||
ReLU 출력: [0, 0, 0.8, 0, ...]</blockquote> | |||
* 이전 층의 활성화 값에 대해, 활성화 함수를 적용하기 전에 평균을 0, 분산을 1에 가깝게 만드는 예시이다. | |||
==수식== | ==수식== | ||
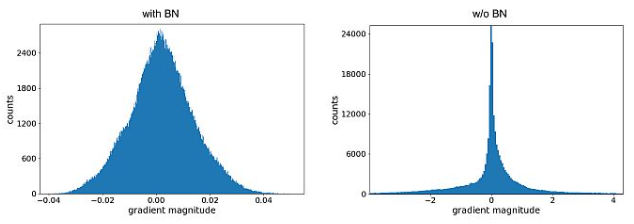
[[파일:배치 정규화 전후 분포.png|섬네일|전후 분포]] | |||
배치 정규화는 다음과 같이 정의된다. | 배치 정규화는 다음과 같이 정의된다. | ||
<blockquote>x̂ = (x - μ<sub>B</sub>) / √(σ<sub>B</sub>² + ε)</blockquote> | '''정규화:'''<blockquote>x̂ = (x - μ<sub>B</sub>) / √(σ<sub>B</sub>² + ε)</blockquote> | ||
*선형 변환: | |||
<blockquote>y = γx̂ + β</blockquote>여기서 | * 풀어 쓰자면 각 입력값에 평균을 빼고, 표준 편차로 나눈다. | ||
* 넓은 범위로 분산된 값을 더 모으는 효과가 있다. | |||
선형 변환:<blockquote>y = γx̂ + β</blockquote>여기서 | |||
*μ<sub>B</sub> : 배치 평균 | *μ<sub>B</sub> : 배치 평균 | ||
*σ<sub>B</sub>² : 배치 분산 | *σ<sub>B</sub>² : 배치 분산 | ||
2025년 10월 25일 (토) 01:36 기준 최신판
배치 정규화(영어: Batch Normalization, 줄여서 BN)는 딥 러닝에서 학습을 안정화하고 속도를 향상시키기 위해 사용되는 정규화 기법이다. 각 층의 입력을 정규화하여 내부 공변량 변화(Internal Covariate Shift)를 줄이는 것을 목적으로 한다.
개요[편집 | 원본 편집]
- 딥러닝 모델은 층이 깊어질수록 학습이 불안정해지고, 기울기 소실/폭주 문제로 인해 학습 속도가 느려진다.
- 배치 정규화는 미니배치 단위로 입력의 평균과 분산을 계산해 정규화한 뒤, 학습 가능한 스케일(scale)과 이동(shift) 파라미터를 적용한다.
- 이 과정을 통해 각 층의 입력 분포를 일정하게 유지하여 학습을 원활히 한다.
예를 들면
Dense 출력값: [-1.2, 0.3, 2.0, -0.8, ...]
↓ BN (정규화)
정규화 후: [-0.9, -0.1, 0.8, -0.5, ...] (평균 ≈ 0)
↓ ReLU
ReLU 출력: [0, 0, 0.8, 0, ...]
- 이전 층의 활성화 값에 대해, 활성화 함수를 적용하기 전에 평균을 0, 분산을 1에 가깝게 만드는 예시이다.
수식[편집 | 원본 편집]
배치 정규화는 다음과 같이 정의된다.
정규화:
x̂ = (x - μB) / √(σB² + ε)
- 풀어 쓰자면 각 입력값에 평균을 빼고, 표준 편차로 나눈다.
- 넓은 범위로 분산된 값을 더 모으는 효과가 있다.
선형 변환:
y = γx̂ + β
여기서
- μB : 배치 평균
- σB² : 배치 분산
- ε : 분모의 0 방지를 위한 작은 값
- γ, β : 학습 가능한 스케일 및 시프트 파라미터
장점[편집 | 원본 편집]
- 학습 속도 향상: 더 큰 학습률(learning rate) 사용 가능
- 기울기 소실/폭주 문제 완화
- 초기화에 대한 의존도 감소
- 정규화 효과로 인해 과적합 방지에 도움
단점[편집 | 원본 편집]
- 미니배치 크기에 의존적이며, 배치가 너무 작으면 통계량 추정이 불안정해진다.
- RNN처럼 시퀀스 의존성이 큰 구조에는 적용이 까다롭다.
- 학습과 추론 단계에서 동작 방식이 달라 관리가 필요하다(추론 시 이동 평균 사용).
변형 기법[편집 | 원본 편집]
- Layer Normalization : 배치가 아닌 개별 샘플 단위로 정규화
- Instance Normalization : 컴퓨터 비전에서 주로 사용, 각 샘플의 채널 단위 정규화
- Group Normalization : 채널을 그룹 단위로 묶어 정규화
응용[편집 | 원본 편집]
- 합성곱 신경망(CNN)에서 필수적으로 사용되는 정규화 기법
- 자연어 처리, 음성 인식 등 다양한 딥러닝 모델에서 안정적인 학습을 위해 적용
같이 보기[편집 | 원본 편집]
참고 문헌[편집 | 원본 편집]
- Sergey Ioffe, Christian Szegedy. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. ICML 2015.
- Ian Goodfellow, Yoshua Bengio, Aaron Courville. Deep Learning. MIT Press, 2016.