합성곱 신경망: 두 판 사이의 차이
IT 위키
편집 요약 없음 |
편집 요약 없음 |
||
| 46번째 줄: | 46번째 줄: | ||
* 최근에는 CNN의 계산 효율성을 개선하기 위해 희소성(sparsity)을 활용한 pruning 기법들이 적극 연구되고 있다. | * 최근에는 CNN의 계산 효율성을 개선하기 위해 희소성(sparsity)을 활용한 pruning 기법들이 적극 연구되고 있다. | ||
== 주요 모델 == | |||
'''[[LeNet]]''' | |||
* LeNet은 1990년대 초반에 제안된 최초의 합성곱 신경망(CNN) 중 하나로, 손글씨 숫자 인식(MNIST) 문제를 해결하기 위해 개발되었다. | |||
* 합성곱(convolution)과 풀링(pooling) 계층을 번갈아 쌓은 뒤 완전연결층을 사용하는 구조를 가지며, 현대 CNN의 기본적인 형태를 제시하였다. | |||
* 당시에는 계산 자원이 제한되어 있었지만, LeNet은 딥러닝 기반 이미지 인식의 가능성을 처음으로 입증한 모델로 평가된다. | |||
'''[[VGG]]''' | |||
*VGG는 매우 작은 3×3 필터를 여러 번 연속으로 쌓는 단순한 구조를 통해 깊이가 성능 향상에 중요한 역할을 한다는 점을 보여주었다. | |||
*단순하고 일관된 설계 덕분에 이후 많은 네트워크의 기반이 되었으며, ImageNet에서 약 75~76%의 높은 정확도를 달성하였다. | |||
*깊은 구조를 가지지만 규칙적인 형태로 인해 구현과 해석이 용이하며, 이후 모델들의 비교 기준으로 자주 사용된다. | |||
'''[[ResNet]]''' | |||
*네트워크의 깊이가 깊어질수록 정확도가 떨어지는 퇴화 문제를 해결하기 위해 잔차 연결(residual link)을 도입하였다. | |||
*입력을 출력에 직접 더하는 shortcut 구조를 통해 학습 안정성을 높이고, 매우 깊은 네트워크에서도 높은 성능을 유지한다. | |||
* 기본 블록과 병목 블록으로 구성되며, ResNet-18, 50, 101 등 다양한 깊이의 변형 모델이 존재한다. | |||
'''[[MobileNet]]''' | |||
*모바일 및 임베디드 기기용으로 설계된 경량 CNN 구조이다. | |||
*표준 합성곱을 깊이별 합성곱(depthwise separable convolution)으로 대체하여 계산량과 파라미터 수를 크게 줄였다. | |||
*MobileNetV2에서는 잔차 구조와 선형 병목(linear bottleneck)을 도입하여 효율성과 성능을 동시에 개선하였다. | |||
'''[[ShuffleNet]]''' | |||
*그룹 합성곱(group convolution)을 사용해 연산량을 줄이면서도 채널 간 정보 교환이 제한되는 문제를 해결하기 위해 채널 셔플(channel shuffle) 연산을 추가하였다. | |||
*모바일 환경에서도 정확도를 유지하며 효율적인 추론이 가능하도록 설계되었다. | |||
*MobileNet과 유사한 수준의 계산 복잡도에서 더 높은 성능을 보인다. | |||
'''[[SqueezeNet]]''' | |||
* AlexNet 수준의 정확도를 50배 적은 파라미터로 달성한 초경량 네트워크이다. | |||
*3×3 필터를 1×1 필터로 대체하고, 입력 채널 수를 줄이는 “fire module” 구조를 사용한다. *모델 크기가 작아 임베디드 시스템이나 IoT 환경에서 사용하기 적합하다. | |||
'''[[DenseNet]]''' | |||
*각 층의 출력을 모든 이후 층과 직접 연결(dense connection)하여 정보 손실을 최소화한다. | |||
*이러한 연결 방식은 특징 재사용(feature reuse)을 촉진하고, 경사 소실(vanishing gradient) 문제를 완화한다. | |||
*파라미터 효율이 높고, 상대적으로 적은 수의 가중치로도 높은 성능을 달성한다. | |||
'''[[EfficientNet]]'''*네트워크의 깊이(depth), 너비(width), 해상도(resolution)를 균형 있게 확장(compound scaling)하는 방식으로 효율적인 모델 확장을 제안하였다. | |||
*동일한 정확도를 더 적은 연산으로 달성하며, 연산 효율이 매우 높다. *SiLU(Swish) 활성함수를 사용하고, 정규화 및 구조적 최적화를 통해 최신 비전 모델들과 경쟁하는 성능을 보인다. | |||
'''[[ConvNeXt]]''' | |||
*비전 트랜스포머(Swin Transformer)의 아이디어를 CNN 구조에 도입한 현대적 합성곱 신경망이다. | |||
*대형 커널, GELU 활성함수, Layer Normalization 등 최신 설계를 적용하여 ResNet을 대체할 수준의 성능을 달성하였다. | |||
*단순한 CNN 구조를 유지하면서도 트랜스포머 수준의 정확도를 보여준다. | |||
'''[[ShiftNet]]''' | |||
*공간 합성곱 연산을 완전히 제거하고, 채널별로 픽셀을 단순 이동(shift)시키는 방식으로 공간 정보를 반영한다. | |||
*연산량(MAC)과 파라미터가 거의 0에 가까운 초경량 구조로, 메모리 대역폭이 제한된 환경에서 효율적이다. | |||
* 계산 비용 없이 합성곱의 효과를 근사화하여 빠른 추론을 지원한다. | |||
==효율화 및 가지치기(Pruning)== | ==효율화 및 가지치기(Pruning)== | ||
CNN의 합성곱 층은 계산 비용이 매우 크므로, 연산 효율을 높이기 위해 다양한 [[가지치기 (딥 러닝)|'''가지치기''']] 방법이 사용된다. | CNN의 합성곱 층은 계산 비용이 매우 크므로, 연산 효율을 높이기 위해 다양한 [[가지치기 (딥 러닝)|'''가지치기''']] 방법이 사용된다. | ||
2025년 10월 25일 (토) 11:11 기준 최신판
- Convolutional Neural Network; 합성곱 인공 신경망; 합성곱신경망
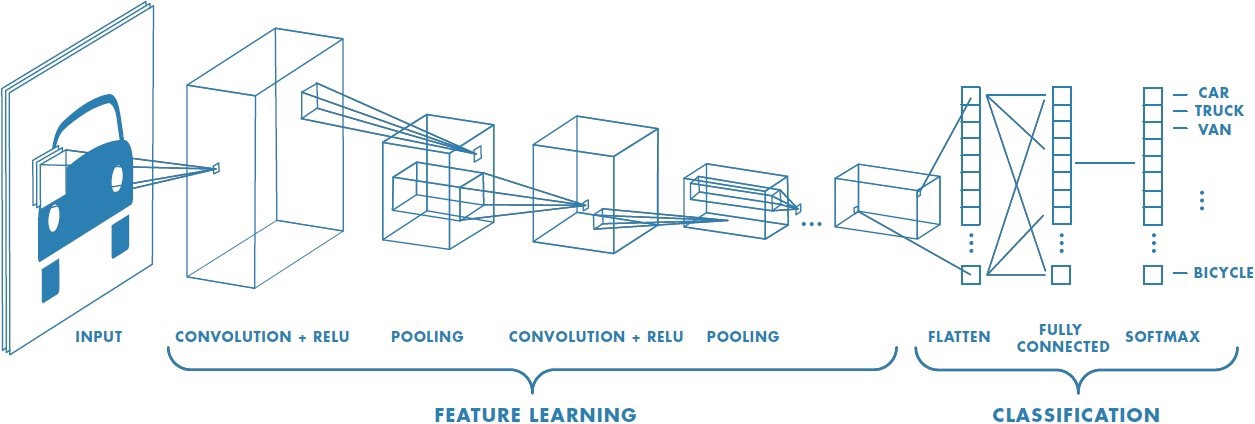
- 합성곱 신경망(Convolutional Neural Network, CNN)은 입력 데이터의 공간적 구조(spatial structure)를 보존하면서 특징(feature)을 자동으로 추출하는 심층 신경망의 한 종류이다.
개요[편집 | 원본 편집]
CNN은 주로 이미지, 영상, 음성, 시계열 데이터 등에서 사용되며, 필터(또는 커널)를 이용해 국소 영역(local receptive field) 내의 패턴을 인식하고 계층적으로 특징을 쌓아 나간다. 다층 퍼셉트론(MLP)이 모든 입력 노드와 연결되는 반면, CNN은 지역 연결성(local connectivity)과 가중치 공유(weight sharing)를 활용하여 파라미터 수를 줄이고 일반화를 향상시킨다. 또한 CNN은 합성곱 연산에서 발생하는 MACs(Multiply-Accumulate Operations)가 연산량의 대부분을 차지하며, 파라미터 효율화 및 가지치기(pruning)가 중요한 연구 주제로 다루어진다.
작동 원리[편집 | 원본 편집]
CNN은 일반적으로 다음과 같은 층들로 구성된다.
합성곱 층 (Convolution Layer)[편집 | 원본 편집]
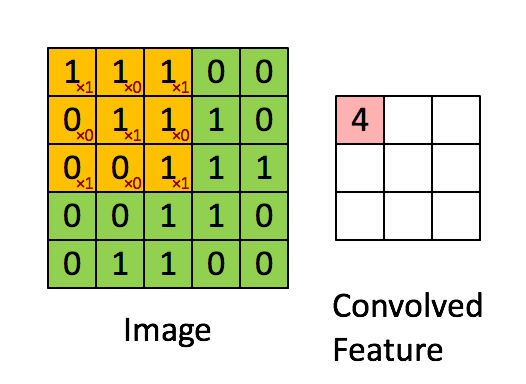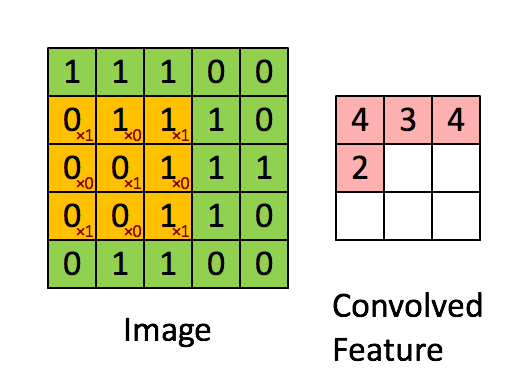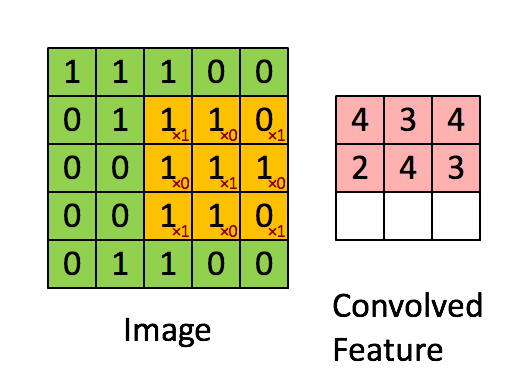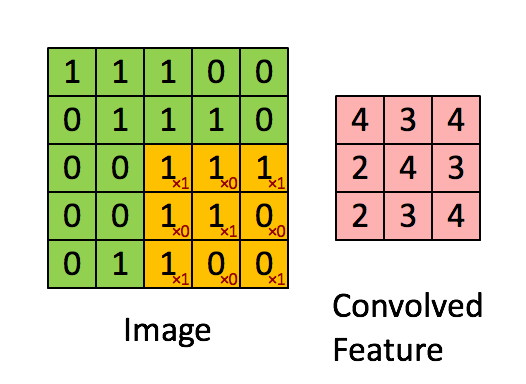
- 입력의 국소 영역에 작용하는 작은 필터(커널)를 사용하여 합성곱 연산을 수행한다.
- 커널이 입력 위를 슬라이딩하면서 입력과 커널 간의 내적을 취해 특징 맵(feature map)을 생성한다.
- 스트라이드(stride), 패딩(padding), 커널 크기 등이 하이퍼파라미터로 사용된다.
- 여러 개의 필터를 사용하면 여러 개의 출력 채널(feature map)을 얻을 수 있다.
- 합성곱 층의 연산량은 보통 다음과 같이 계산된다:
- MACs = (필터 수) × (채널 수) × (필터 높이) × (필터 너비) × (출력 높이) × (출력 너비)
활성화 함수 (Activation)[편집 | 원본 편집]
- 일반적으로 ReLU(Rectified Linear Unit)가 많이 쓰이며, 입력 값을 비선형으로 변환하여 비선형 표현력을 부여한다.
- 다른 활성화 함수도 사용 가능하다 (sigmoid, tanh 등).
풀링 층 (Pooling Layer)[편집 | 원본 편집]
- 공간 크기를 감소시켜 연산량을 줄이고 특징의 불변성(invariance)을 강화한다.
- 대표적으로 max pooling, average pooling 등이 있다.
- 예: 2×2 영역에서 최대값을 취하는 max pooling 방식이 흔히 사용된다.
완전 연결층 (Fully Connected Layer)[편집 | 원본 편집]
- 최종적으로 추출된 특징 벡터를 입력으로 받아 분류(classification) 또는 회귀(regression)를 수행하는 층이다.
- 소프트맥스(softmax) 계층을 통해 확률 분포로 변환되는 경우가 많다.
기타 기법들[편집 | 원본 편집]
- 드롭아웃(dropout), 배치 정규화(batch normalization) 등을 통해 과적합(overfitting)을 방지
- 전이 학습(transfer learning)을 위해 사전 학습된 CNN을 활용
- 다운샘플링을 위한 스트라이드 사용
- 확장 합성곱(dilated convolution), 전치 합성곱(transposed convolution) 등 다양한 변형
- CNN의 학습 중 Network Slimming 기법을 적용하여 Batch Normalization의 스케일링 인자를 기준으로 불필요한 채널을 제거할 수 있음.
역사 및 발전[편집 | 원본 편집]
- 최초의 합성곱 신경망 개념은 “네오코그니트론(Neocognitron)”에서 출발하였다.
- LeNet-5는 손글씨 숫자 인식용으로 1990년대에 제안된 초기 CNN 모형이다.
- 2012년, AlexNet은 GPU 학습을 활용해 ImageNet 대회에서 큰 성능 향상을 보이며 딥러닝 붐을 이끌었다.
- 이후 VGG, ResNet, Inception, EfficientNet 등 다양한 구조가 등장하였다.
- 최근에는 CNN의 계산 효율성을 개선하기 위해 희소성(sparsity)을 활용한 pruning 기법들이 적극 연구되고 있다.
주요 모델[편집 | 원본 편집]
- LeNet은 1990년대 초반에 제안된 최초의 합성곱 신경망(CNN) 중 하나로, 손글씨 숫자 인식(MNIST) 문제를 해결하기 위해 개발되었다.
- 합성곱(convolution)과 풀링(pooling) 계층을 번갈아 쌓은 뒤 완전연결층을 사용하는 구조를 가지며, 현대 CNN의 기본적인 형태를 제시하였다.
- 당시에는 계산 자원이 제한되어 있었지만, LeNet은 딥러닝 기반 이미지 인식의 가능성을 처음으로 입증한 모델로 평가된다.
- VGG는 매우 작은 3×3 필터를 여러 번 연속으로 쌓는 단순한 구조를 통해 깊이가 성능 향상에 중요한 역할을 한다는 점을 보여주었다.
- 단순하고 일관된 설계 덕분에 이후 많은 네트워크의 기반이 되었으며, ImageNet에서 약 75~76%의 높은 정확도를 달성하였다.
- 깊은 구조를 가지지만 규칙적인 형태로 인해 구현과 해석이 용이하며, 이후 모델들의 비교 기준으로 자주 사용된다.
- 네트워크의 깊이가 깊어질수록 정확도가 떨어지는 퇴화 문제를 해결하기 위해 잔차 연결(residual link)을 도입하였다.
- 입력을 출력에 직접 더하는 shortcut 구조를 통해 학습 안정성을 높이고, 매우 깊은 네트워크에서도 높은 성능을 유지한다.
- 기본 블록과 병목 블록으로 구성되며, ResNet-18, 50, 101 등 다양한 깊이의 변형 모델이 존재한다.
- 모바일 및 임베디드 기기용으로 설계된 경량 CNN 구조이다.
- 표준 합성곱을 깊이별 합성곱(depthwise separable convolution)으로 대체하여 계산량과 파라미터 수를 크게 줄였다.
- MobileNetV2에서는 잔차 구조와 선형 병목(linear bottleneck)을 도입하여 효율성과 성능을 동시에 개선하였다.
- 그룹 합성곱(group convolution)을 사용해 연산량을 줄이면서도 채널 간 정보 교환이 제한되는 문제를 해결하기 위해 채널 셔플(channel shuffle) 연산을 추가하였다.
- 모바일 환경에서도 정확도를 유지하며 효율적인 추론이 가능하도록 설계되었다.
- MobileNet과 유사한 수준의 계산 복잡도에서 더 높은 성능을 보인다.
- AlexNet 수준의 정확도를 50배 적은 파라미터로 달성한 초경량 네트워크이다.
- 3×3 필터를 1×1 필터로 대체하고, 입력 채널 수를 줄이는 “fire module” 구조를 사용한다. *모델 크기가 작아 임베디드 시스템이나 IoT 환경에서 사용하기 적합하다.
- 각 층의 출력을 모든 이후 층과 직접 연결(dense connection)하여 정보 손실을 최소화한다.
- 이러한 연결 방식은 특징 재사용(feature reuse)을 촉진하고, 경사 소실(vanishing gradient) 문제를 완화한다.
- 파라미터 효율이 높고, 상대적으로 적은 수의 가중치로도 높은 성능을 달성한다.
EfficientNet*네트워크의 깊이(depth), 너비(width), 해상도(resolution)를 균형 있게 확장(compound scaling)하는 방식으로 효율적인 모델 확장을 제안하였다.
- 동일한 정확도를 더 적은 연산으로 달성하며, 연산 효율이 매우 높다. *SiLU(Swish) 활성함수를 사용하고, 정규화 및 구조적 최적화를 통해 최신 비전 모델들과 경쟁하는 성능을 보인다.
- 비전 트랜스포머(Swin Transformer)의 아이디어를 CNN 구조에 도입한 현대적 합성곱 신경망이다.
- 대형 커널, GELU 활성함수, Layer Normalization 등 최신 설계를 적용하여 ResNet을 대체할 수준의 성능을 달성하였다.
- 단순한 CNN 구조를 유지하면서도 트랜스포머 수준의 정확도를 보여준다.
- 공간 합성곱 연산을 완전히 제거하고, 채널별로 픽셀을 단순 이동(shift)시키는 방식으로 공간 정보를 반영한다.
- 연산량(MAC)과 파라미터가 거의 0에 가까운 초경량 구조로, 메모리 대역폭이 제한된 환경에서 효율적이다.
- 계산 비용 없이 합성곱의 효과를 근사화하여 빠른 추론을 지원한다.
효율화 및 가지치기(Pruning)[편집 | 원본 편집]
CNN의 합성곱 층은 계산 비용이 매우 크므로, 연산 효율을 높이기 위해 다양한 가지치기 방법이 사용된다.
Weight Pruning (가중치 가지치기)[편집 | 원본 편집]
- 특정 비율의 가중치를 0으로 만들어 희소(sparse) 행렬을 형성.
- 연산량은 (1-p) 배로 감소 (p는 제거된 비율).
- 희소 가중치는 메모리 효율적으로 저장할 수 있음.
Activation Pruning (활성화 가지치기)[편집 | 원본 편집]
- ReLU 등으로 인해 출력 활성값이 50% 이상 0이 되는 경우 많음.
- 입력 활성화도 pruning하면 연산량을 추가 절감 가능.
- 단, 온라인 처리가 필요해 추가적인 정렬 비용이 발생.
Structured vs. Unstructured Pruning[편집 | 원본 편집]
- Unstructured pruning: 개별 weight 제거 → 정확도 손실이 적지만 하드웨어 최적화 어려움.
- Structured pruning: 필터, 채널 단위로 제거 → 하드웨어 친화적이지만 정확도 손해 발생.
- N:M sparsity: 구조화와 비구조화의 절충안 (예: 2:4 sparsity, 4개 중 2개 유지). Nvidia V100 GPU에서 지원됨.
Network Slimming[편집 | 원본 편집]
- Batch Normalization의 스케일링 인자에 L1 정규화를 추가해 불필요한 채널을 자동 식별.
- 학습 과정에서 자연스럽게 중요하지 않은 채널이 제거됨.
Cascade Effect (계단식 효과)[편집 | 원본 편집]
- 한 층에서 필터가 제거되면, 다음 층에서도 입력 채널 수가 줄어 추가 희소성이 발생.
- CNN의 pruning은 단일 레이어가 아니라 연속된 레이어에 파급효과를 미침.
응용 분야[편집 | 원본 편집]
CNN은 다음과 같은 분야에서 널리 응용된다.
- 이미지 분류 및 인식 (예: 개/고양이 구분)
- 객체 검출 (object detection)
- 이미지 분할 (semantic segmentation)
- 스타일 변환(style transfer), 이미지 생성
- 의료 영상 처리 (예: MRI, CT 영상 분석)
- 음성 및 시계열 데이터 처리
장점과 한계[편집 | 원본 편집]
장점[편집 | 원본 편집]
- 공간 구조를 보존하면서 특징을 추출 가능
- 파라미터 수가 상대적으로 적어 학습이 효율적
- 지역 특징과 계층적 특징을 자동 학습
- Pruning 기법을 활용하면 CNN의 연산 및 저장 비용을 더욱 줄일 수 있음
한계 및 도전 과제[편집 | 원본 편집]
- 많은 데이터와 연산 자원이 필요
- 입력 위치 변화에 대한 민감성 (약한 불변성)
- 과적합 문제
- 해석 가능성 문제 (왜 특정 필터가 학습되었는지 설명이 어려움)
- Activation pruning은 계산량이 커서 실시간 적용이 어려움
최근 동향 및 변형 모델[편집 | 원본 편집]
구조적 변형[편집 | 원본 편집]
- 완전 합성곱 신경망(fully convolutional network, FCN)은 입력 크기에 관계없이 출력 맵을 만드는 구조로 세그멘테이션 등에 사용된다.
- U-Net은 의료 영상 분할 분야에서 특히 많이 쓰인다.
- 확장 합성곱(dilated convolution), 심층 분리 합성곱(depthwise separable convolution), 그룹 합성곱(group convolution) 등 다양한 변형 구조가 제안되었다.
- G-CNN 등의 대칭성 기반 일반화 기법도 연구되고 있다.
효율 향상 모델[편집 | 원본 편집]
- EfficientNet은 Compound Scaling을 통해 적은 파라미터 수로도 정확성과 효율성을 높인 대표적인 CNN 모델이다.
- EfficientDet은 EfficientNet을 backbone으로 하고 BiFPN과 Compound Scaling을 조합하여 Object Detection에서 효율적인 성능을 낸다.
- 최근에는 CNN과 Transformer를 결합하거나 pruning을 통해 경량화된 형태로 발전하는 추세도 있다.
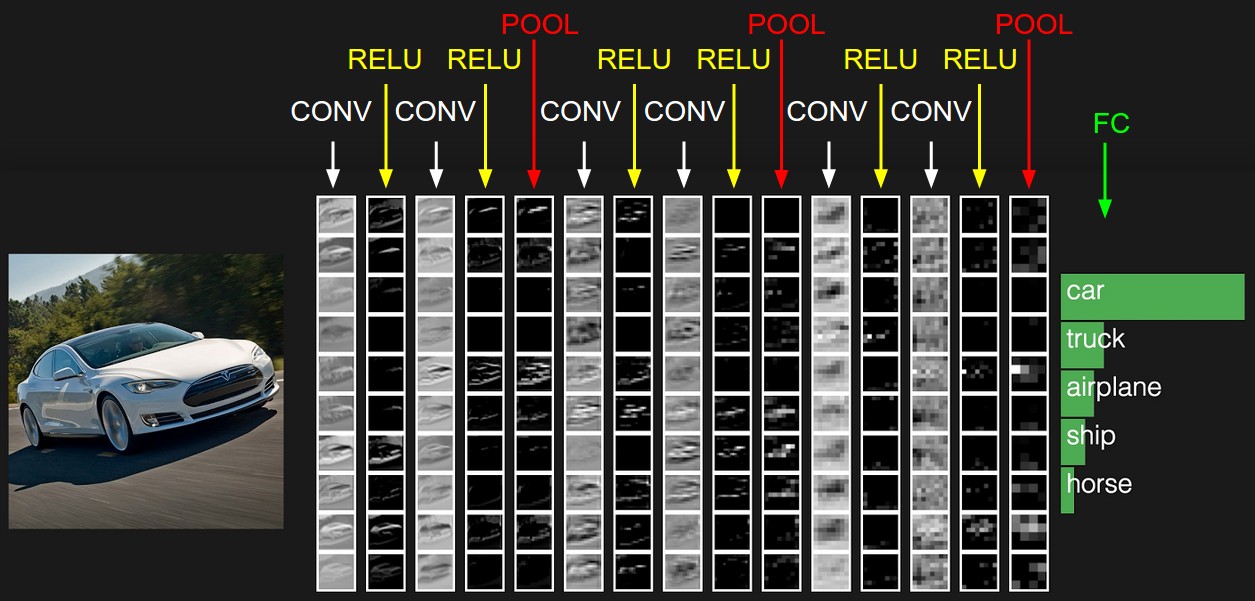
CNN 처리 과정 도식화[편집 | 원본 편집]
- 실제 이미지 CNN 처리 과정 예시
구성 및 절차[편집 | 원본 편집]
- 대상을 채널별로 나누고, 정보 손실 방지를 위해 패딩을 적용한 후, 필터를 이용해 스트라이드 단위로 합성곱을 해서 피처 맵을 만들어냄. 빠른 처리를 위해 풀링 적용
- 채널(Channel)
- 패딩(Padding)
- 필터(Filter), 커널(Kernel)
- 합성곱(Convolution)
- 스트라이드(Stride)
- 액티베이션 맵(Activation Map)
- 풀링(Pooling) 레이어
- 피처 맵(Feature Map)
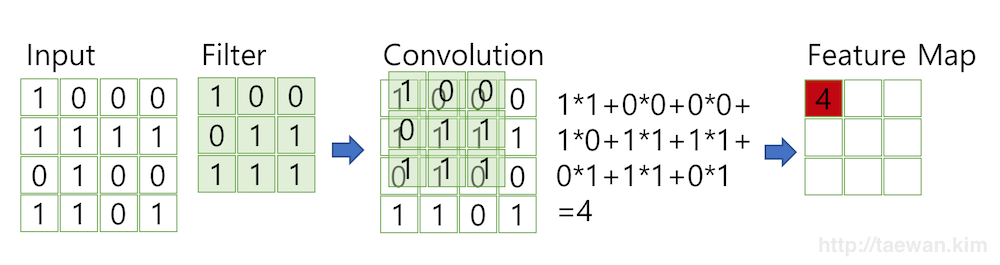
합성곱[편집 | 원본 편집]
- Convolution
- 이미지에 필터를 합성곱으로 적용
- 각 행렬 값을 곱하여 합산
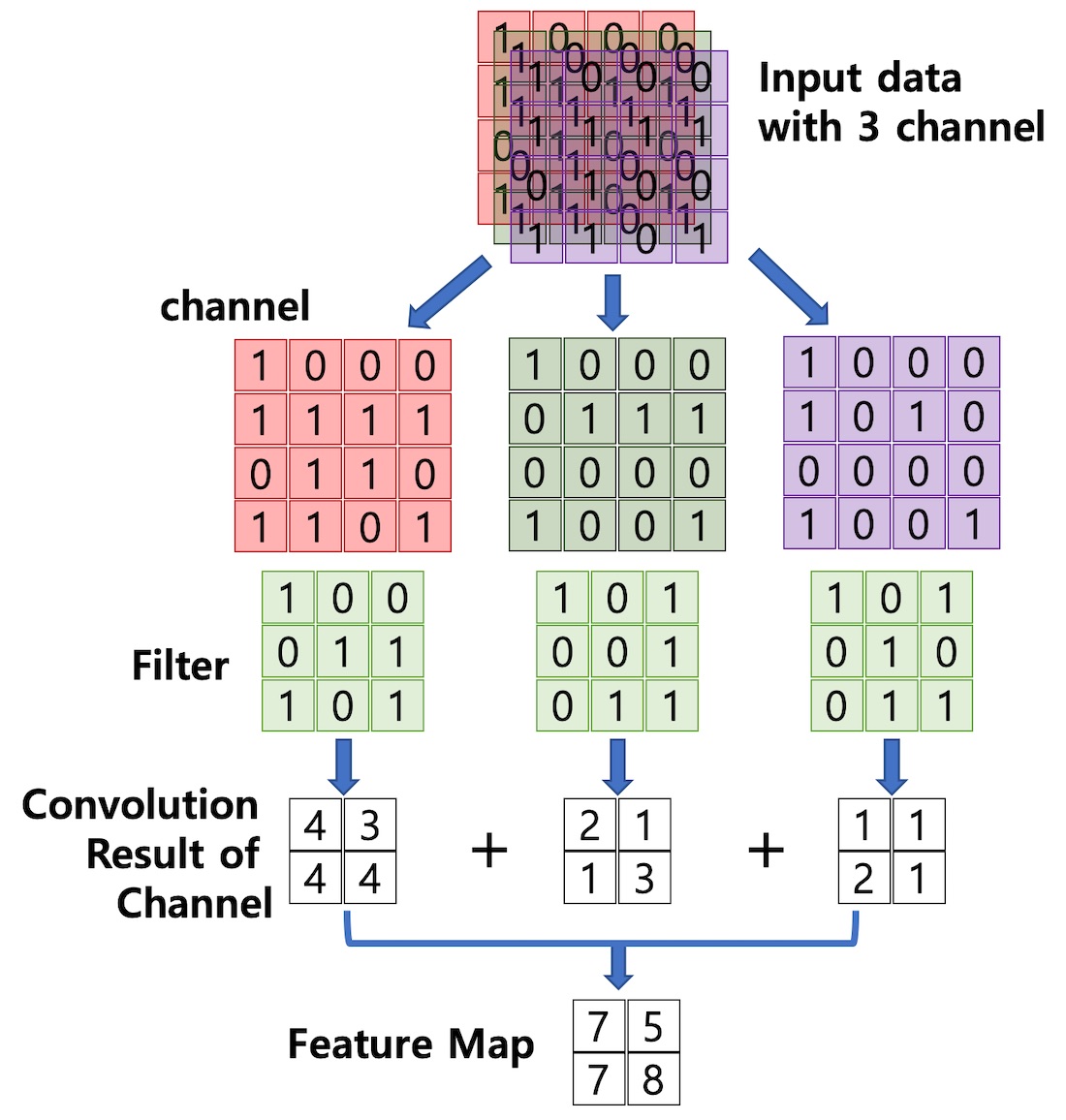
채널[편집 | 원본 편집]
- Channel
- 컬러 그림의 RGB 구분
- Red 채널, Green 채널, Blue 채널
- 여러 채널에 걸친 합성곱 생성 절차
패딩[편집 | 원본 편집]
- Padding
- 데이터 소실 및 경계 표현을 위한 테두리
필터[편집 | 원본 편집]
- Filter; 커널(Kernel)과 같은 의미로 쓰임
- 이미지의 특징을 찾아내기 위한 공용 파라미터
풀링과 피처 맵[편집 | 원본 편집]
- Pooling & Feature Map
- 컨볼루션 레이어의 출력 데이터(Activation Map)의 크기를 줄이거나 특정 데이터를 강조
- Max Pooling과 Average Pooling, Min Pooling이 있는데, Max Pooling을 많이 사용
참고 문헌[편집 | 원본 편집]
- CNN, Convolutional Neural Network 요약
- Hoefler, Torsten, et al. "Sparsity in deep learning: Pruning and growth for efficient inference and training in neural networks." JMLR, 2021.
- Liu, Zhuang, et al. "Learning efficient convolutional networks through network slimming." ICCV, 2017.
- Kung, H. T., et al. "Packing sparse convolutional neural networks for efficient systolic array implementations." ASPLOS, 2019.