볼록 껍질 (알고리즘): 두 판 사이의 차이
IT 위키
AlanTuring (토론 | 기여) (새 문서: 볼록 껍질(Convex Hull)은 2차원 평면상의 여러 점 집합에서, '''모든 점을 포함하는 가장 작은 볼록 다각형'''을 의미한다. 쉽게 말해, 고무줄을 점들에 감쌌을 때 만들어지는 가장 바깥쪽 경계를 뜻하며, 계산기하학에서 매우 기본적이고 중요한 문제다. ==개념== *점들이 모여 있는 형태에서 '''가장 바깥쪽을 둘러싸는 볼록 다각형'''을 찾는 문제 *볼록 다각형이란 두 점...) |
AlanTuring (토론 | 기여) 편집 요약 없음 |
||
| 3번째 줄: | 3번째 줄: | ||
*점들이 모여 있는 형태에서 '''가장 바깥쪽을 둘러싸는 볼록 다각형'''을 찾는 문제 | *점들이 모여 있는 형태에서 '''가장 바깥쪽을 둘러싸는 볼록 다각형'''을 찾는 문제 | ||
*볼록 다각형이란 두 점을 잇는 선분이 항상 다각형 내부에 포함되는 다각형을 의미함 | *볼록 다각형이란 두 점을 잇는 선분이 항상 다각형 내부에 포함되는 다각형을 의미함 | ||
*입력: n개의 점 (x, y) | *'''입력''': n개의 점 (x, y) | ||
*출력: 볼록 껍질을 이루는 점들의 리스트 (반시계 방향 정렬) | *'''출력''': 볼록 껍질을 이루는 점들의 리스트 (반시계 방향 정렬) | ||
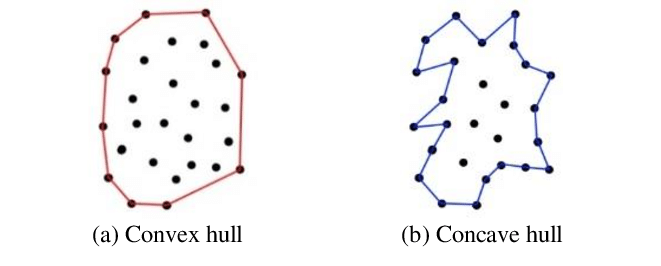
*'''목적''': 가장 작은 다각형을 찾는 것이 목적이다. 가장 작다는 것은 일반적으로 테두리의 길이가 가장 작고 연결하는 꼭지점의 수가 작은 것을 의미한다. 아래 그림을 보면 면적은 (b)가 더 작지만 대부분의 알고리즘에서는 (a)를 최적의 답으로 선택한다. | |||
[[파일:볼록 껍질의 예시.png|400x400픽셀]] | |||
==응용== | ==응용== | ||
*컴퓨터 그래픽스 및 시각화 | *컴퓨터 그래픽스 및 시각화 | ||
| 14번째 줄: | 17번째 줄: | ||
*입력 점들을 극각 기준으로 정렬 후 스택을 이용해 볼록 껍질 생성 | *입력 점들을 극각 기준으로 정렬 후 스택을 이용해 볼록 껍질 생성 | ||
*시간 복잡도: O(n log n) | *시간 복잡도: O(n log n) | ||
절차: | '''절차:''' | ||
#가장 y값이 작은 점을 기준점으로 설정 | #가장 y값이 작은 점을 기준점으로 설정 | ||
#나머지 점들을 기준점에서의 각도(극각) 기준으로 정렬 | #나머지 점들을 기준점에서의 각도(극각) 기준으로 정렬 | ||
2025년 4월 5일 (토) 00:57 판
볼록 껍질(Convex Hull)은 2차원 평면상의 여러 점 집합에서, 모든 점을 포함하는 가장 작은 볼록 다각형을 의미한다. 쉽게 말해, 고무줄을 점들에 감쌌을 때 만들어지는 가장 바깥쪽 경계를 뜻하며, 계산기하학에서 매우 기본적이고 중요한 문제다.
개념
- 점들이 모여 있는 형태에서 가장 바깥쪽을 둘러싸는 볼록 다각형을 찾는 문제
- 볼록 다각형이란 두 점을 잇는 선분이 항상 다각형 내부에 포함되는 다각형을 의미함
- 입력: n개의 점 (x, y)
- 출력: 볼록 껍질을 이루는 점들의 리스트 (반시계 방향 정렬)
- 목적: 가장 작은 다각형을 찾는 것이 목적이다. 가장 작다는 것은 일반적으로 테두리의 길이가 가장 작고 연결하는 꼭지점의 수가 작은 것을 의미한다. 아래 그림을 보면 면적은 (b)가 더 작지만 대부분의 알고리즘에서는 (a)를 최적의 답으로 선택한다.
응용
- 컴퓨터 그래픽스 및 시각화
- 충돌 감지, 경계 영역 계산
- 지도 서비스에서의 범위 검색
- 패턴 인식, 머신러닝의 군집 경계 계산
대표 알고리즘
1. Graham Scan
- 입력 점들을 극각 기준으로 정렬 후 스택을 이용해 볼록 껍질 생성
- 시간 복잡도: O(n log n)
절차:
- 가장 y값이 작은 점을 기준점으로 설정
- 나머지 점들을 기준점에서의 각도(극각) 기준으로 정렬
- 시계 방향 회전하는 점은 제거하고 반시계 방향 점만 스택에 유지
2. Andrew's Monotone Chain
- 점들을 x좌표 기준으로 정렬 후, 위쪽 껍질과 아래쪽 껍질을 각각 생성 후 병합
- 시간 복잡도: O(n log n)
3. Jarvis March (Gift Wrapping)
- 가장 왼쪽 점에서 시작하여 시계방향으로 외접하는 점을 차례로 선택
- 시간 복잡도: O(nh) (h는 볼록 껍질에 속한 점의 수)
- 작은 h에서는 빠름
4. Chan's Algorithm
- Graham Scan과 Jarvis March를 결합
- 시간 복잡도: O(n log h) — 이론적으로 가장 효율적
파이썬 예시 (Graham Scan)
def ccw(p1, p2, p3):
return (p2[0]-p1[0])*(p3[1]-p1[1]) - (p2[1]-p1[1])*(p3[0]-p1[0])
def graham_scan(points):
points = sorted(points, key=lambda p: (p[1], p[0]))
pivot = points[0]
sorted_pts = sorted(points[1:], key=lambda p: (atan2(p[1]-pivot[1], p[0]-pivot[0]), p))
hull = [pivot]
for pt in sorted_pts:
while len(hull) >= 2 and ccw(hull[-2], hull[-1], pt) <= 0:
hull.pop()
hull.append(pt)
return hull
같이 보기
참고 문헌
- Cormen, T. H., Leiserson, C. E., Rivest, R. L., & Stein, C. (2009). Introduction to Algorithms. MIT Press
- Computational Geometry: Algorithms and Applications by de Berg et al.
- https://cp-algorithms.com/geometry/convex-hull.html