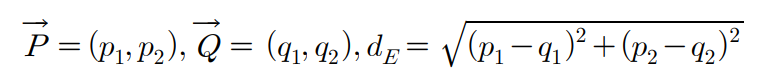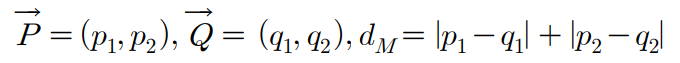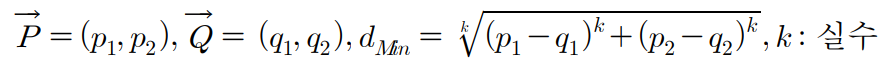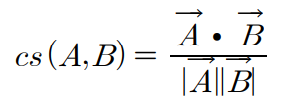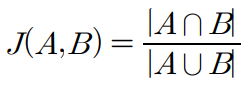벡터 유사도
유클리드 거리[편집 | 원본 편집]
Euclidean distance
두 점 사이의 거리를 구하는 가장 대표적인 방식이다. 구하는 방식은 두 벡터에서 각 성분 간의 차를 제곱하여 합한 뒤 제곱근을 씌워 구한다. 벡터 P와 Q 사이의 유클리드 거리는 아래와 같이 나타낼 수 있다.
맨해튼 거리[편집 | 원본 편집]
Manhattan distance
흔히 택시 거리라고도 하며, 거리 공간에서 유클리드 거리 외의 두 점 사이의 거리를 구하는 방식으로 알려져있다. 두 벡터가 있을 때, 벡터 성분 간 차이의 절댓값을 모두 합하여 구하므로 유클리드 거리보다 식이 비교적 간단하다. 벡터 P와 Q 사이의 맨해튼 거리를 식으로 나타내면 아래와 같다.
민코프스키 거리[편집 | 원본 편집]
Minkowski distance
두 벡터의 유사도를 벡터 사이의 각도를 사용해 표현하는 방식이다. 두 벡터 사이의 각도는 0도에서 최대 180도가 가능하며, 이때 그 각도에 해당하는 코사인 값을 두 벡터 사이의 코사인 유사도로 정의한다. 코사인 유사도 값을 구하는 식은 벡터의 내적을 사용해 아래와 같이 표현할 수 있다.
거리 공간에서 사용하는 거리 함수들을 일반화한 방식으로 생각할 수 있다. 아래와 같은 식으로 표현하며, p가 1인 경우 맨해튼 거리, p가 2인 경우 유클리드 거리와 동일하게 표현된다.
코사인 유사도[편집 | 원본 편집]
Cosine similarity
두 벡터의 유사도를 벡터 사이의 각도를 사용해 표현하는 방식이다. 두 벡터 사이의 각도는 0도에서 최대 180도가 가능하며, 이때 그 각도에 해당하는 코사인 값을 두 벡터 사이의 코사인 유사도로 정의한다. 코사인 유사도 값을 구하는 식은 벡터의 내적을 사용해 아래와 같이 표현할 수 있다.
자카드 유사도[편집 | 원본 편집]
Jaccard similarity
두 개의 집합 사이에서 유사도를 구하는 방식이다. 두 집합의 합집합과 교집합의 크기의 비율 값을 유사도로 나타내어 1에 가까울수록 두 집합이 유사한 원소를 가지고 있음을 알 수 있다. 아래의 식은 집합 A와 B 사이의 자카드 유사도를 나타낸 식이다.
참고 문헌[편집 | 원본 편집]
- 출처: FoolsGold 알고리즘의 취약점 분석 및 해결 방안 모색(김호, 박시찬, 신홍직, 이정호, 임준환)