분할 정복 알고리즘

Divide and Conquer

분할 정복이란 크고 방대한 문제를 작은 단위로 나눠가며 해결하고 다시 합쳐나감으로써 결과를 도출하는 접근법을 말한다. 많은 알고리즘이 분할 정복 방법을 사용하고 있으며, 특정 알고리즘이라기 보다는 방법론에 해당한다. Divide and Conquer Algorithm은 분할 정복 방법론을 사용한 퀵소트, 병합정렬 등의 알고리즘들을 지칭하는 말이 될 수 있다.

어원은 로마 제국이 식민지인들의 단결을 막기 위해 주로 사용한 방법으로 유명한 분할 통치(Divide and Rule)이다.

개요[편집 | 원본 편집]

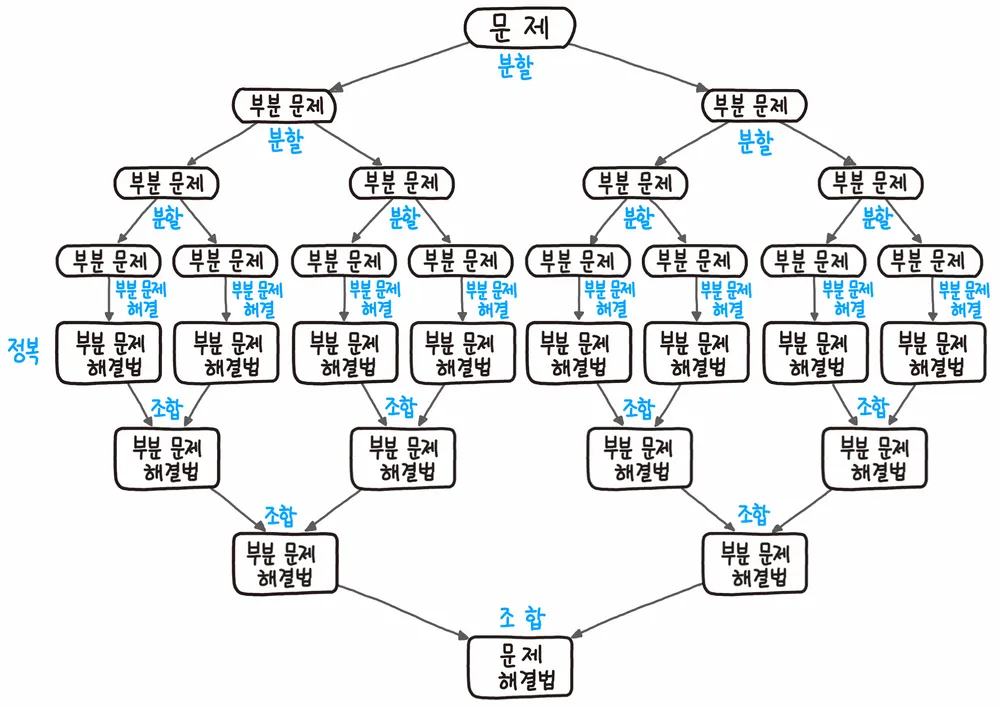
그림에서와 같이 분할 정복은 상단에서 분할하고 중앙에서 정복하고 하단에서 조합(Combine)하는 형태로 도식화 할 수 있다.

분할: 문제를 더이상 분할할 수 없을 때까지 동일한 유형의 여러 하위 문제로 나눈다.
정복: 가장 작은 단위의 하위 문제를 해결하여 정복한다.
조합: 하위 문제에 대한 결과를 원래 문제에 대한 결과로 조합한다.

폰 노이만이 병합 정렬을 통해 분할 정복을 설명한 것은 1945년이었는데, 사실 문제를 축소해서 정복한다는 개념의 역사는 훨씬 더 이전인 기원 전까지 거슬러 올라간다. 고대 그리스의 수학자 유클리드(Euclid)는 자신이 저술한 『원론』에서 문제를 분할해 풀이하는 최대 공약수 알고리즘을 정리했으며, 이 유클리드 알고리즘은 인류 최초의 알고리즘으로 일컬어진다.

또한 뉴턴도 분할 정복과 비슷한 아이디어로 미분을 개발했다. 잘게 쪼개어 합한후 극한으로 보낸다는 말은 고등학교 수학시간에 주구장창 들었을것이다.

적용 예시[편집 | 원본 편집]

분할 정복법은 재귀적으로 자신을 호출하면서 그 연산의 단위를 조금씩 줄어가는 방식이다. 분할 정복의 프로세스는 대체로 아래와 같다.

function F(x):
  if F(x)가 간단 then:
    return F(x)를 계산한 값
  else:
    x 를 x1, x2로 분할
    F(x1)과 F(x2)를 호출
    return F(x1), F(x2)로 F(x)를 구한 값

한 마디로 "F(x)가 간단"이라는 조건을 만족할 때까지 문제를 쪼개고 쪼개서 값을 구하자는 것이다.

장단점[편집 | 원본 편집]

장점[편집 | 원본 편집]

문제를 나누어 처리함으로써 한번에 처리하기 어려운 문제를 해결할 수 있다는 장점이 있다. 그리고 이 방식이 그대로 사용되는 효율적인 알고리즘들도 여럿 있으며, 문제를 나누어 해결한다는 특징상 병렬적으로 문제를 해결하는 데 큰 강점이 있다.

단점[편집 | 원본 편집]

함수를 재귀적으로 호출한다는 점에서 함수 호출로 인한 오버헤드가 발생하며, 스택에 다양한 데이터를 보관하고 있어야 하므로 스택 오버플로우가 발생하거나 과도한 메모리 사용을 하게 되는 단점이 있다. 가장 중요한 것은 이 알고리즘의 핵심인 "F(x)가 간단"이 어떤 것이냐에 따라 알고리즘의 퍼포먼스가 생각보다 꽤 차이나게 된다는 것이다. 이 "F(x)가 간단하다"라는 것을 정의하는 것의 난해함 역시 단점 중에서 중요하게 다루어지고 있다.