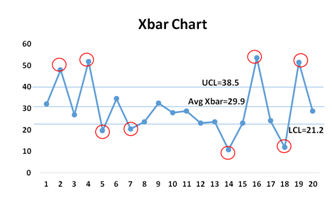
X-bar 차트

X-bar 차트는 통계적 공정 관리(SPC, Statistical Process Control)에서 사용되는 관리도의 일종으로, 공정의 중심 위치(평균값)가 통계적으로 안정적인지를 모니터링하는 데 사용된다. 측정형(계량형) 품질 특성에 적합하며, 일반적으로 R-차트 또는 S-차트와 함께 사용된다.

개요

X-bar 차트는 일정한 간격으로 채취한 샘플들의 평균값을 기반으로 하며, 시간에 따른 공정 평균의 변화 여부를 감지한다. 공정이 통계적으로 안정 상태에 있다면, 측정된 평균값들은 중심선(CL) 주위에서 일정한 범위 내에 분포하게 된다.

구성 요소

• CL (중심선)
  • 전체 샘플 평균
  • CL = X̄̄ (모든 샘플의 평균값들의 평균)

• UCL (상한선)
  • UCL = X̄̄ + A₂ × R̄

• LCL (하한선)
  • LCL = X̄̄ - A₂ × R̄

여기서,

• X̄̄: 모든 샘플 평균의 평균
• R̄: 모든 샘플 범위(Range)의 평균
• A₂: 샘플 크기(n)에 따라 결정되는 상수 (표로 제공됨)

사용 조건

• 연속적인 계량형 데이터(예: 길이, 무게 등)
• 샘플 크기가 일정해야 함 (보통 n = 2~10)
• 변동이 비교적 작고 정규 분포를 가정할 수 있는 데이터

예시

공정에서 5개씩 샘플을 25회 채취한 경우:

• 각 샘플의 평균을 계산하여 점으로 표시
• 전체 샘플의 평균(X̄̄)과 범위 평균(R̄)을 구한 뒤, A₂ 값을 적용하여 UCL, LCL 계산
• X-bar 차트에 각 평균값을 시계열로 표시하여 공정의 평균이 안정 상태인지 확인

관리도 비교

다양한 관리도의 특징을 다음과 같이 요약할 수 있다.

관리도 유형	측정 대상	데이터 종류	샘플 크기 제약	목적
X-bar 차트	평균값	계량형	일정해야 함	공정의 평균(중심) 추적
R-차트	범위(Range)	계량형	일정해야 함	공정의 변동성 추적 (소샘플)
S-차트	표준편차(Standard deviation)	계량형	일정해야 함	공정의 변동성 추적 (대샘플)
P-차트	불량률	계수형(불량/양품)	일정하지 않아도 가능	공정의 비율 변화 추적
NP-차트	불량 개수	계수형(불량/양품)	일정해야 함	공정의 불량 개수 추적

장점

• 공정의 중심 위치(평균값) 변화 감지에 용이함
• 실시간 모니터링에 적합
• R-차트, S-차트와 함께 사용하면 평균과 변동을 동시에 통제 가능

단점

• 공정의 산포가 불안정한 경우 단독 사용은 부적절함 (R 또는 S 차트와 병행 필요)
• 데이터가 정규분포를 따르지 않으면 부정확한 결과가 나올 수 있음

같이 보기

• 통계적 공정 관리
• R-차트
• S-차트
• 관리도
• P-차트
• 품질 관리

참고 문헌

• Montgomery, D. C. (2012). Introduction to Statistical Quality Control. Wiley.
• 이재원. (2019). 품질경영론. 형설출판사.