AVL 트리: 두 판 사이의 차이
IT 위키
AlanTuring (토론 | 기여) 편집 요약 없음 |
AlanTuring (토론 | 기여) (→Python) |
||
| 39번째 줄: | 39번째 줄: | ||
== 구현 코드 == | == 구현 코드 == | ||
=== Python === | === Python === | ||
<syntaxhighlight lang=" | <syntaxhighlight lang="python3"> | ||
class Node: | class Node: | ||
def __init__(self, key): | def __init__(self, key): | ||
| 84번째 줄: | 84번째 줄: | ||
balance = self.get_balance(root) | balance = self.get_balance(root) | ||
if balance > 1 and key < root.left.key: | if balance > 1 and key < root.left.key: | ||
return self.right_rotate(root) | return self.right_rotate(root) | ||
if balance < -1 and key > root.right.key: | if balance < -1 and key > root.right.key: | ||
return self.left_rotate(root) | return self.left_rotate(root) | ||
if balance > 1 and key > root.left.key: | if balance > 1 and key > root.left.key: | ||
root.left = self.left_rotate(root.left) | root.left = self.left_rotate(root.left) | ||
return self.right_rotate(root) | return self.right_rotate(root) | ||
if balance < -1 and key < root.right.key: | if balance < -1 and key < root.right.key: | ||
root.right = self.right_rotate(root.right) | root.right = self.right_rotate(root.right) | ||
| 103번째 줄: | 99번째 줄: | ||
return root | return root | ||
def min_value_node(self, node): | |||
current = node | |||
while current.left: | |||
current = current.left | |||
return current | |||
def delete(self, root, key): | |||
if not root: | |||
return root | |||
if key < root.key: | |||
root.left = self.delete(root.left, key) | |||
elif key > root.key: | |||
root.right = self.delete(root.right, key) | |||
else: | |||
if not root.left: | |||
return root.right | |||
elif not root.right: | |||
return root.left | |||
temp = self.min_value_node(root.right) | |||
root.key = temp.key | |||
root.right = self.delete(root.right, temp.key) | |||
if not root: | |||
return root | |||
root.height = max(self.get_height(root.left), self.get_height(root.right)) + 1 | |||
balance = self.get_balance(root) | |||
if balance > 1 and self.get_balance(root.left) >= 0: | |||
return self.right_rotate(root) | |||
if balance > 1 and self.get_balance(root.left) < 0: | |||
root.left = self.left_rotate(root.left) | |||
return self.right_rotate(root) | |||
if balance < -1 and self.get_balance(root.right) <= 0: | |||
return self.left_rotate(root) | |||
if balance < -1 and self.get_balance(root.right) > 0: | |||
root.right = self.right_rotate(root.right) | |||
return self.left_rotate(root) | |||
return root | |||
def lookup(self, root, key): | |||
if not root or root.key == key: | |||
return root | |||
if key < root.key: | |||
return self.lookup(root.left, key) | |||
return self.lookup(root.right, key) | |||
def pre_order(self, root): | |||
if root: | |||
print(root.key, end=" ") | |||
self.pre_order(root.left) | |||
self.pre_order(root.right) | |||
# AVL 트리 테스트 | # AVL 트리 테스트 | ||
| 109번째 줄: | 164번째 줄: | ||
for key in [10, 20, 30, 40, 50, 25]: | for key in [10, 20, 30, 40, 50, 25]: | ||
root = avl.insert(root, key) | root = avl.insert(root, key) | ||
print("Preorder traversal after insertions:") | |||
avl.pre_order(root) | |||
print("\n") | |||
# Lookup test | |||
search_key = 25 | |||
found_node = avl.lookup(root, search_key) | |||
print(f"Lookup {search_key}: {'Found' if found_node else 'Not found'}") | |||
# Deleting a node | |||
delete_key = 20 | |||
root = avl.delete(root, delete_key) | |||
print(f"\nPreorder traversal after deleting {delete_key}:") | |||
avl.pre_order(root) | |||
print("\n") | |||
</syntaxhighlight> | </syntaxhighlight> | ||
== 같이 보기 == | == 같이 보기 == | ||
{{틀:데이터베이스 인덱스 트리}} | {{틀:데이터베이스 인덱스 트리}} | ||
2025년 2월 13일 (목) 08:31 판
- Adelson-Velskii and Landis Tree
- 트리내 각각의 노드마다 1 이하의 균형치(Balance Factor, +1,0,1)를 가지기 위해, 삽입과 삭제를 할때마다 균형치를 검사하여 RR, LL, LR, RL 회전연산을 시행하는 이진탐색트리
- 발표자인 1962년 G.M. Adelson-Velskii와 E.M. Landis 가 그들의 이름을 따서 명명
특징
- 한 노드를 중심으로 좌우 종속 트리의 높이 차가 1 이하인 균형 잡힌 트리
- 이진 트리의 삽입·삭제 과정에서 한 방향으로 치우치거나, 높이 차이로 인해서 수행 시간이 증가되는 것을 막기 위해 균형 유지
- B 트리 등과 함께 균형잡힌 트리(height-balanced tree)라고도 불림
균형 인수
균형 인수(Balance Factor, BF)는 노드의 왼쪽 서브트리와 오른쪽 서브트리의 높이 차이를 의미한다.
| 균형 인수 (BF) | 트리 상태 |
|---|---|
| -1, 0, 1 | 균형 상태 (Balanced) |
| < -1 또는 > 1 | 불균형 상태 (Unbalanced, 회전 필요) |
회전 동작
개요
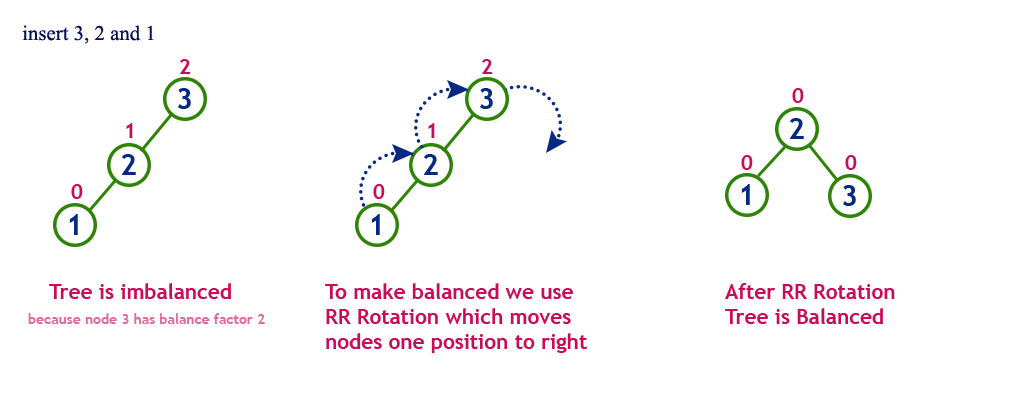
- LL 회전: A 로부터 N 까지의 경로상의 노드들을 오른쪽으로 회전
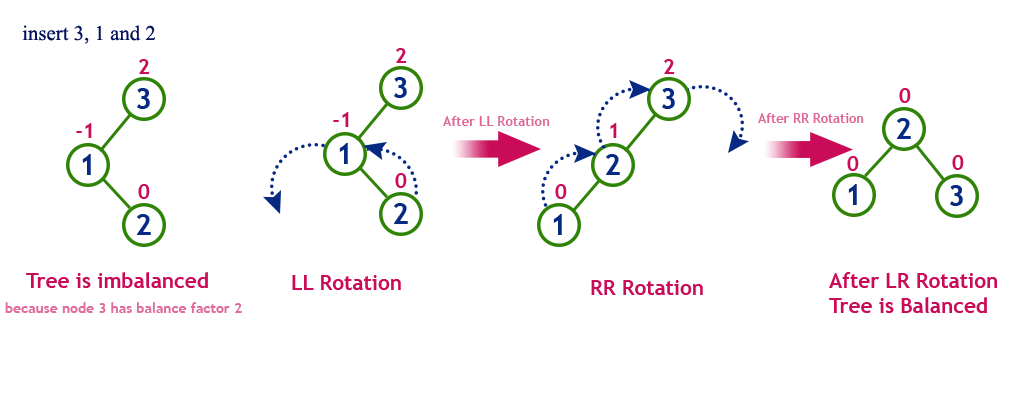
- LR 회전: A 로부터 N 까지의 경로상의 노드들을 왼쪽-오른쪽으로 회전
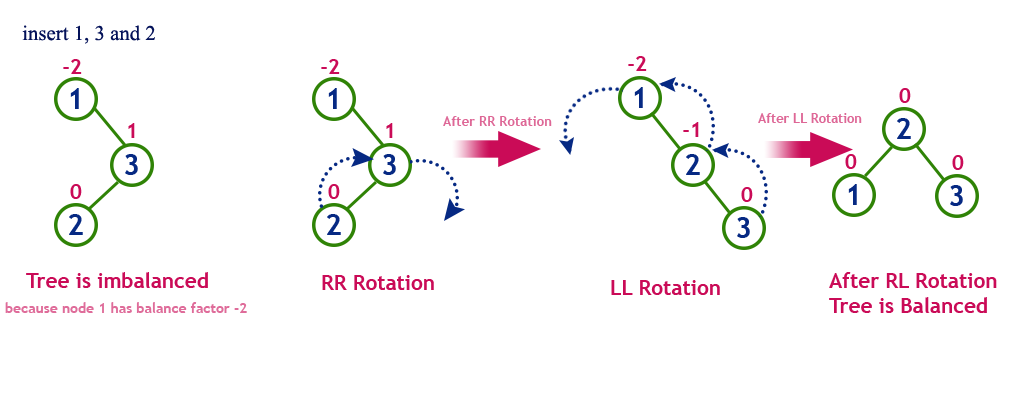
- RL 회전: A 로부터 N 까지의 경로상의 노드들을 오른쪽-왼쪽으로 회전
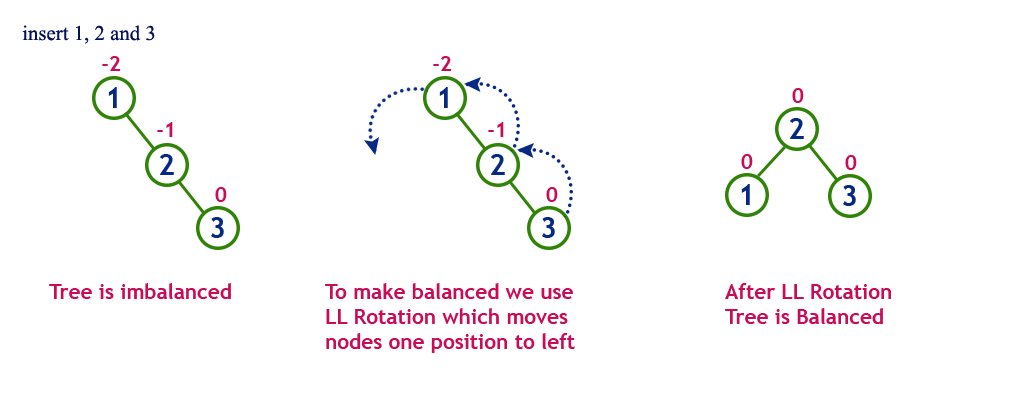
- RR 회전: A 로부터 N 까지의 경로상의 노드들을 왼쪽으로 회전
동작 예시
- RR 회전
- LR 회전
- RL 회전
- LL 회전
구현 코드
Python
class Node:
def __init__(self, key):
self.key = key
self.left = None
self.right = None
self.height = 1
class AVLTree:
def get_height(self, node):
return node.height if node else 0
def get_balance(self, node):
return self.get_height(node.left) - self.get_height(node.right) if node else 0
def right_rotate(self, z):
y = z.left
T3 = y.right
y.right = z
z.left = T3
z.height = max(self.get_height(z.left), self.get_height(z.right)) + 1
y.height = max(self.get_height(y.left), self.get_height(y.right)) + 1
return y
def left_rotate(self, z):
y = z.right
T2 = y.left
y.left = z
z.right = T2
z.height = max(self.get_height(z.left), self.get_height(z.right)) + 1
y.height = max(self.get_height(y.left), self.get_height(y.right)) + 1
return y
def insert(self, root, key):
if not root:
return Node(key)
if key < root.key:
root.left = self.insert(root.left, key)
else:
root.right = self.insert(root.right, key)
root.height = max(self.get_height(root.left), self.get_height(root.right)) + 1
balance = self.get_balance(root)
if balance > 1 and key < root.left.key:
return self.right_rotate(root)
if balance < -1 and key > root.right.key:
return self.left_rotate(root)
if balance > 1 and key > root.left.key:
root.left = self.left_rotate(root.left)
return self.right_rotate(root)
if balance < -1 and key < root.right.key:
root.right = self.right_rotate(root.right)
return self.left_rotate(root)
return root
def min_value_node(self, node):
current = node
while current.left:
current = current.left
return current
def delete(self, root, key):
if not root:
return root
if key < root.key:
root.left = self.delete(root.left, key)
elif key > root.key:
root.right = self.delete(root.right, key)
else:
if not root.left:
return root.right
elif not root.right:
return root.left
temp = self.min_value_node(root.right)
root.key = temp.key
root.right = self.delete(root.right, temp.key)
if not root:
return root
root.height = max(self.get_height(root.left), self.get_height(root.right)) + 1
balance = self.get_balance(root)
if balance > 1 and self.get_balance(root.left) >= 0:
return self.right_rotate(root)
if balance > 1 and self.get_balance(root.left) < 0:
root.left = self.left_rotate(root.left)
return self.right_rotate(root)
if balance < -1 and self.get_balance(root.right) <= 0:
return self.left_rotate(root)
if balance < -1 and self.get_balance(root.right) > 0:
root.right = self.right_rotate(root.right)
return self.left_rotate(root)
return root
def lookup(self, root, key):
if not root or root.key == key:
return root
if key < root.key:
return self.lookup(root.left, key)
return self.lookup(root.right, key)
def pre_order(self, root):
if root:
print(root.key, end=" ")
self.pre_order(root.left)
self.pre_order(root.right)
# AVL 트리 테스트
avl = AVLTree()
root = None
for key in [10, 20, 30, 40, 50, 25]:
root = avl.insert(root, key)
print("Preorder traversal after insertions:")
avl.pre_order(root)
print("\n")
# Lookup test
search_key = 25
found_node = avl.lookup(root, search_key)
print(f"Lookup {search_key}: {'Found' if found_node else 'Not found'}")
# Deleting a node
delete_key = 20
root = avl.delete(root, delete_key)
print(f"\nPreorder traversal after deleting {delete_key}:")
avl.pre_order(root)
print("\n")