스킵 리스트

스킵 리스트(skip list)는 정렬된 원소를 빠르게 탐색, 삽입, 삭제할 수 있도록 설계된 확률적 자료구조이다. 1989년 William Pugh가 제안하였으며, 연결 리스트(linked list)의 구조를 확장하여 이진 탐색 트리 수준의 효율성을 얻을 수 있도록 고안되었다.

1 개요

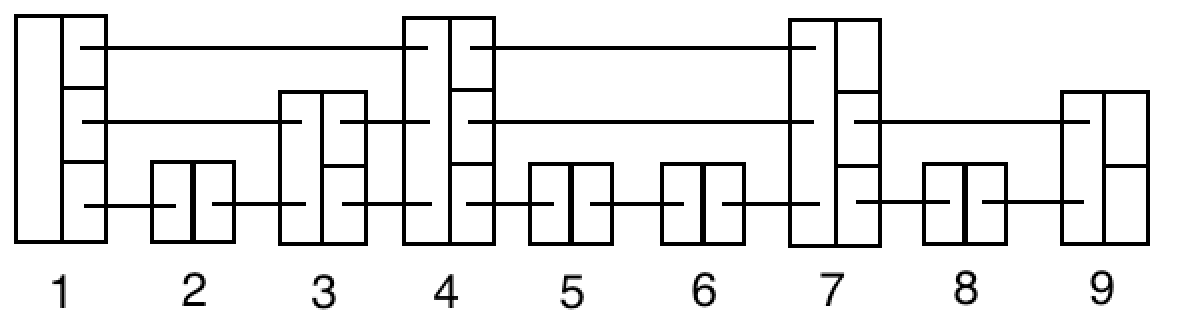
스킵 리스트는 여러 수준의 연결 리스트를 위로 확장한 구조를 가진다. 기본 연결 리스트는 가장 하위 레벨에 존재하며, 그 위로 확률적으로 선택된 노드들만 포함하는 상위 레벨들이 존재한다. 각 노드는 자신이 속한 레벨의 다음 노드를 가리키는 포인터를 가진다. 탐색, 삽입, 삭제 등의 연산은 상위 레벨부터 내려가며 진행되어, 일반 연결 리스트보다 빠른 속도를 제공한다.

2 구조

스킵 리스트는 레벨(level)의 개념을 기반으로 구성된다.

• Level 0: 전체 원소를 포함하는 기본 연결 리스트
• Level 1 이상: 일정 확률(p, 일반적으로 1/2 또는 1/4)에 따라 무작위로 선택된 노드만 포함
• Head node: 모든 레벨의 시작점을 포함하는 특수 노드

노드마다 여러 개의 포인터가 있으며, 자신의 레벨 수에 따라 상위 레벨까지 연결된다.

3 연산

• 탐색
  • 최상위 레벨부터 오른쪽으로 이동하며, 목표 값을 초과하기 전까지 진행한 후, 아래로 내려가 다시 탐색을 반복한다.
• 삽입
  • 삽입 위치를 찾은 후, 랜덤하게 레벨을 결정하고 해당 위치에 새 노드를 추가한다.
• 삭제
  • 탐색을 통해 대상 노드를 찾고, 해당 노드를 포함한 모든 레벨에서 포인터를 조정하여 제거한다.

4 시간 복잡도

스킵 리스트는 다음과 같은 평균 시간 복잡도를 갖는다.

• 탐색: O(log n)
• 삽입: O(log n)
• 삭제: O(log n)

최악의 경우 O(n)일 수 있으나, 확률적 구조 덕분에 평균적으로는 균형잡힌 이진 탐색 트리와 유사한 성능을 가진다.

5 예제

다음은 Python에서 간단한 스킵 리스트 노드 구조의 예시이다.

import random

class SkipNode:
    def __init__(self, key, level):
        self.key = key
        self.forward = [None] * (level + 1)

class SkipList:
    def __init__(self, max_level, p):
        self.max_level = max_level
        self.p = p
        self.header = SkipNode(None, max_level)
        self.level = 0

    def random_level(self):
        lvl = 0
        while random.random() < self.p and lvl < self.max_level:
            lvl += 1
        return lvl

6 장점

• 간단한 구현으로도 이진 탐색 트리 수준의 성능 달성
• 포인터 조작만으로 동적 삽입, 삭제에 용이
• 동시성 제어가 상대적으로 쉬움 (Lock-free skip list 구현 등)

7 단점

• 공간 사용량 증가 (다수의 포인터 필요)
• 성능이 확률에 의존함

8 같이 보기

• 이진 탐색 트리
• 연결 리스트
• 해시 테이블
• AVL 트리
• 동시성 제어

9 참고 문헌

• William Pugh (1990). "Skip Lists: A Probabilistic Alternative to Balanced Trees". Communications of the ACM.
• Cormen, T. H., Leiserson, C. E., Rivest, R. L., and Stein, C. (2009). Introduction to Algorithms. MIT Press.